The Stability of High Order Max-Type Difference Equation

Han Cai-hong; Li Lue; Tan Xue

doi:doi:10.11648/j.acm.20160502.13

| Peer-Reviewed

The Stability of High Order Max-Type Difference Equation

Han Cai-hong, Li Lue, Tan Xue

Published in Applied and Computational Mathematics (Volume 5, Issue 2)

Received: 6 April 2016 Accepted: Published: 7 April 2016

Views: Downloads:

Download PDF

Share This Article

Twitter
Linked In
Facebook

Abstract

In this paper, we investigate the stability of following max-type difference equation 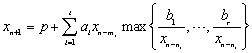, where , with , , and , the initial values are positive. By constructing a system of equations and binary function, we show the equation has a unique positive equilibrium solution, and the positive equilibrium solution is globally asymptotically stable. The conclusion of this paper extends and supplements the existing results.

Published in	Applied and Computational Mathematics (Volume 5, Issue 2)
DOI	10.11648/j.acm.20160502.13
Page(s)	51-55
Creative Commons	This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited.
Copyright	Copyright © The Author(s), 2024. Published by Science Publishing Group

Keywords

Difference Equations, Positive Solution, Convergence, Globally Stable

References

[1]	El-Metwally H, “Global behavior of an economic model,” Chaos Solitons & Fractals, 33(3), 2007, pp. 994-1005.
[2]	El-Metwally H, El-Afifi M M, “On the behavior of some extension forms of some population Models,” Chaos Solitons & Fractals, 36(1), 2008, pp. 104-114.
[3]	Zhou L, Honghua H U, Liang C, et al, “Research on difference equation model in traffic flow calculation,” Journal of Chang chun University of Science & Technology, 2014, pp. 117-123.
[4]	Huang C M, Wang W P, “Applications of difference equation in population forecasting model,” Advanced Materials Research, 2014, pp. 1079-1080.
[5]	Berenhaut K, Foley J, S. Stević S, “The global attractivity of the rational difference equation ,” Proceedings of the American Mathematical Society, 135, 2007, pp. 1133-1140.
[6]	Berenhaut K S, Stević S, “The behavior of the positive solutions of the difference equation ,” J. Journal of Difference Equations and Applications, 12(9), 2006, pp. 909-918.
[7]	Berg L, Stević S, “Periodicity of some classes of holomorphic difference equations,” Journal of Difference Equations and Applications, 12(8), 2006, pp. 827-835.
[8]	Iričanin B, Stević S, “Some systems of nonlinear difference equations of higher order with periodic solutions,” Dynamics of Continuous Discrete and Impulsive Systems Series, 13A (3-4), 2006, pp. 499–507.
[9]	Iričanin B, Stević S, “Eventually constant solutions of a rationa ldifference equation,” Applied Mathematics and Computation, 215, 2009, pp. 854-856.
[10]	Elabbasy E M, El-Metwally H A, Elsayed E M, “Global behavior of the solutions of some difference equations,” Advances in Difference Equations, 28(2), 2011, pp. 683-689.
[11]	Elsayed E M, Iričanin B, Stević S, “On the max-type equation ,” Ars Combinatoria, 95, 2010, pp. 187-192.
[12]	Stević S, “Global stability of a max-type difference equation,” Applied Mathematics & Computation, 216(1), 2010, pp. 354–356.
[13]	Sun T X, Xi H J, Han C H, “Dynamics of the max-type difference equation ,” Journal of Applied Mathematics and Computing, 2012 (1-2), 2012, pp. 173-180.
[14]	Stević S, “On a symmetric system of max-type difference Equations,” Applied Mathematics and Computation, 219(15), 2013, pp. 8407-8412.
[15]	Stević S, “On some periodic systems of max-type difference equations,” Applied Mathematics and Computation, 218, 2012, pp. 11483–11487.
[16]	Amleh A M, Georgiou D A, Grove E A, Ladas G, “On the recursive sequence ,” Journal of Mathematital Analysis and applications, 233(2), 1999, pp. 790-798.
[17]	Fan Y, Wang L, Li W, “Global behavior of a higher order nonlinear diference equation,” Journal of Mathematital Analysis and applications, 299(1), 2004, pp. 113-126.
[18]	Sun T X, He Q L, Wua X, Xi H J, “Global behavior of the max-type difference equation ,” Applied Mathematics and Computation, 248, 2014, pp. 687-692.
[19]	Liu W P, Stević S, “Global attractivity of a family of non-autonomous max-type difference equations,” Applied Mathematics and Computation, 218(11), 2012, pp. 6297-9303.
[20]	Grove E A, Ladas G, Periodicities in Nonlinear Difference Equations, Vol. 4, New York: Chapman& Hall/CRC Press, 2005, pp. 2.

Cite This Article

Plain Text BibTeX RIS

APA Style

Han Cai-hong, Li Lue, Tan Xue. (2016). The Stability of High Order Max-Type Difference Equation. Applied and Computational Mathematics, 5(2), 51-55. https://doi.org/10.11648/j.acm.20160502.13

Copy | Download

ACS Style

Han Cai-hong; Li Lue; Tan Xue. The Stability of High Order Max-Type Difference Equation. Appl. Comput. Math. 2016, 5(2), 51-55. doi: 10.11648/j.acm.20160502.13

Copy | Download

AMA Style

Han Cai-hong, Li Lue, Tan Xue. The Stability of High Order Max-Type Difference Equation. Appl Comput Math. 2016;5(2):51-55. doi: 10.11648/j.acm.20160502.13

Copy | Download

@article{10.11648/j.acm.20160502.13,
  author = {Han Cai-hong and Li Lue and Tan Xue},
  title = {The Stability of High Order Max-Type Difference Equation},
  journal = {Applied and Computational Mathematics},
  volume = {5},
  number = {2},
  pages = {51-55},
  doi = {10.11648/j.acm.20160502.13},
  url = {https://doi.org/10.11648/j.acm.20160502.13},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.acm.20160502.13},
  abstract = {In this paper, we investigate the stability of following max-type difference equation , where , with , ,  and , the initial values are positive. By constructing a system of equations and binary function, we show the equation has a unique positive equilibrium solution, and the positive equilibrium solution is globally asymptotically stable. The conclusion of this paper extends and supplements the existing results.},
 year = {2016}
}

Copy | Download

TY  - JOUR
T1  - The Stability of High Order Max-Type Difference Equation
AU  - Han Cai-hong
AU  - Li Lue
AU  - Tan Xue
Y1  - 2016/04/07
PY  - 2016
N1  - https://doi.org/10.11648/j.acm.20160502.13
DO  - 10.11648/j.acm.20160502.13
T2  - Applied and Computational Mathematics
JF  - Applied and Computational Mathematics
JO  - Applied and Computational Mathematics
SP  - 51
EP  - 55
PB  - Science Publishing Group
SN  - 2328-5613
UR  - https://doi.org/10.11648/j.acm.20160502.13
AB  - In this paper, we investigate the stability of following max-type difference equation , where , with , ,  and , the initial values are positive. By constructing a system of equations and binary function, we show the equation has a unique positive equilibrium solution, and the positive equilibrium solution is globally asymptotically stable. The conclusion of this paper extends and supplements the existing results.
VL  - 5
IS  - 2
ER  -

Copy | Download

Author Information

Han Cai-hong

School of Mathematics and Statistics, Guangxi Normal University, Guilin, China
Li Lue

School of Mathematics and Statistics, Guangxi Normal University, Guilin, China
Tan Xue

School of Mathematics and Statistics, Guangxi Normal University, Guilin, China

Download PDF

Sections

Plain Text BibTeX RIS

APA Style

Han Cai-hong, Li Lue, Tan Xue. (2016). The Stability of High Order Max-Type Difference Equation. Applied and Computational Mathematics, 5(2), 51-55. https://doi.org/10.11648/j.acm.20160502.13

Copy | Download

ACS Style

Han Cai-hong; Li Lue; Tan Xue. The Stability of High Order Max-Type Difference Equation. Appl. Comput. Math. 2016, 5(2), 51-55. doi: 10.11648/j.acm.20160502.13

Copy | Download

AMA Style

Han Cai-hong, Li Lue, Tan Xue. The Stability of High Order Max-Type Difference Equation. Appl Comput Math. 2016;5(2):51-55. doi: 10.11648/j.acm.20160502.13

Copy | Download

@article{10.11648/j.acm.20160502.13,
  author = {Han Cai-hong and Li Lue and Tan Xue},
  title = {The Stability of High Order Max-Type Difference Equation},
  journal = {Applied and Computational Mathematics},
  volume = {5},
  number = {2},
  pages = {51-55},
  doi = {10.11648/j.acm.20160502.13},
  url = {https://doi.org/10.11648/j.acm.20160502.13},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.acm.20160502.13},
  abstract = {In this paper, we investigate the stability of following max-type difference equation , where , with , ,  and , the initial values are positive. By constructing a system of equations and binary function, we show the equation has a unique positive equilibrium solution, and the positive equilibrium solution is globally asymptotically stable. The conclusion of this paper extends and supplements the existing results.},
 year = {2016}
}

Copy | Download

TY  - JOUR
T1  - The Stability of High Order Max-Type Difference Equation
AU  - Han Cai-hong
AU  - Li Lue
AU  - Tan Xue
Y1  - 2016/04/07
PY  - 2016
N1  - https://doi.org/10.11648/j.acm.20160502.13
DO  - 10.11648/j.acm.20160502.13
T2  - Applied and Computational Mathematics
JF  - Applied and Computational Mathematics
JO  - Applied and Computational Mathematics
SP  - 51
EP  - 55
PB  - Science Publishing Group
SN  - 2328-5613
UR  - https://doi.org/10.11648/j.acm.20160502.13
AB  - In this paper, we investigate the stability of following max-type difference equation , where , with , ,  and , the initial values are positive. By constructing a system of equations and binary function, we show the equation has a unique positive equilibrium solution, and the positive equilibrium solution is globally asymptotically stable. The conclusion of this paper extends and supplements the existing results.
VL  - 5
IS  - 2
ER  -

Copy | Download