1. Introduction
The term robot means different things to different people. Science fiction books and movies have strongly influenced what many people expect a robot to be or what it can do. Sadly the practice of robotics is far behind this popular conception
| [1] | P. Corke, “Robotics, Vision and Control Fundamental Algorithms in MATLAB®,” 2nd Edition, Springer Springer-Verlag, Heidelberg, 2017. |
[1]
. Basically, the design, implementation and control of any class or type of robots present a challenge to the designer
| [1] | P. Corke, “Robotics, Vision and Control Fundamental Algorithms in MATLAB®,” 2nd Edition, Springer Springer-Verlag, Heidelberg, 2017. |
| [2] | P. H. Petkov, T. N. Slavov and J. K. Kralev “Design of Embedded Robust Control Systems Using MATLAB®/Simulink®,” The Institution of Engineering and Technology, London, United Kingdom, 2018. |
| [3] | C. S. Chin, “Computer-Aided Control System Design: Practical Applications Using MATLAB® and Simulink®,” CRC Press - Taylor & Francis Group, Raton, USA, 2013. |
[1-3]
. In particular, the design of two-wheeled robot control system represents a challenge to the designer
| [2] | P. H. Petkov, T. N. Slavov and J. K. Kralev “Design of Embedded Robust Control Systems Using MATLAB®/Simulink®,” The Institution of Engineering and Technology, London, United Kingdom, 2018. |
[2]
. The robot motion in horizontal and vertical planes is described by a nonlinear model whose derivation may be a difficult task
| [1] | P. Corke, “Robotics, Vision and Control Fundamental Algorithms in MATLAB®,” 2nd Edition, Springer Springer-Verlag, Heidelberg, 2017. |
| [2] | P. H. Petkov, T. N. Slavov and J. K. Kralev “Design of Embedded Robust Control Systems Using MATLAB®/Simulink®,” The Institution of Engineering and Technology, London, United Kingdom, 2018. |
| [3] | C. S. Chin, “Computer-Aided Control System Design: Practical Applications Using MATLAB® and Simulink®,” CRC Press - Taylor & Francis Group, Raton, USA, 2013. |
[1-3]
. The linearization of this model leads to unstable non-minimum phase plant which should be stabilized in the presence of parameter variations, noises, and disturbances
| [2] | P. H. Petkov, T. N. Slavov and J. K. Kralev “Design of Embedded Robust Control Systems Using MATLAB®/Simulink®,” The Institution of Engineering and Technology, London, United Kingdom, 2018. |
| [4] | K. Ogata, “Modern Control Engineering,” Pearson Education, Inc., Prentice Hall, Upper Saddle River, New Jersey, USA, 2010. |
| [5] | W. S. Levine, “The Control Handbook: Control System Advanced Methods,” Second Edition, CRC Press - Taylor & Francis Group, New York, USA, 2011. |
| [6] | N. S. Nise, “Control Systems Engineering,” Seventh Edition, John Wiley & Sons Inc., California, USA. |
[2, 4-6]
.
During the last few years a growing interest was observed in using laboratory devices in control education. Among different designs robotic and oscillatory devices have become most popular
| [1] | P. Corke, “Robotics, Vision and Control Fundamental Algorithms in MATLAB®,” 2nd Edition, Springer Springer-Verlag, Heidelberg, 2017. |
| [2] | P. H. Petkov, T. N. Slavov and J. K. Kralev “Design of Embedded Robust Control Systems Using MATLAB®/Simulink®,” The Institution of Engineering and Technology, London, United Kingdom, 2018. |
| [3] | C. S. Chin, “Computer-Aided Control System Design: Practical Applications Using MATLAB® and Simulink®,” CRC Press - Taylor & Francis Group, Raton, USA, 2013. |
| [7] | A. A. Bobtsov, A. A. Pyrkin, S. A. Kolyubin, S. V. Shavetov, S. A. Chepinskiy, Y. A. Kapitanyuk, A. A. Kapitonov, V. M. Bardov, A. V. Titov and M. O. Surov, “Using of LEGO Mindstorms NXT Technology for Teaching of Basics of Adaptive Control Theory,” IFAC Proceedings Volumes, vol. 44, no. 1, pp. 9818-9823, 2011. |
[1-3, 7]
. New practical problems such as the control of networks and cyber-physical systems demand both for new theory and for new design and education means. Fortunately, the developments of computer technologies lead to creation of convenient computation and communication environments, supporting design and education.
One of the recent milestones on this way is LEGO Mindstorms NXT
| [7] | A. A. Bobtsov, A. A. Pyrkin, S. A. Kolyubin, S. V. Shavetov, S. A. Chepinskiy, Y. A. Kapitanyuk, A. A. Kapitonov, V. M. Bardov, A. V. Titov and M. O. Surov, “Using of LEGO Mindstorms NXT Technology for Teaching of Basics of Adaptive Control Theory,” IFAC Proceedings Volumes, vol. 44, no. 1, pp. 9818-9823, 2011. |
| [8] | S. A. Fillippov, A. L. Fradkov, I. V. Ashikhmina and R. E. Seifullaev, “LEGO Mindstorms NXT Robot and Oscillators in Control Education,” IFAC Proceedings Volumes, vol. 43, no. 11, pp. 156-160, 2010. |
| [9] | B. A. Aleexeevich, A. K. Yuri, A. K. Alexander, A. K. Sergey, P. A. Alexandrovich, A. C. Sergey and V. S. Sergey, “LEGO Mindstorms NXT for Teaching the Principles of Adaptive Control to Students,” Sci. & Tech. J. of Inf. Tech., Mech. and Opt., vol. 355, no. 1(71), pp. 103-108, 2011. |
| [10] | M. Canale and S. Casale-Brunet, “A multidisciplinary approach for Model Predictive Control Education: A Lego Mindstorms NXT-based framework,” Int. J. of Cont., Aut. & Sys, vol. 12, no. 5, pp. 1030 - 1039, 2014. https://doi.org/10.1007/s12555-013-0282-7 |
[7-10]
. The LEGO Mindstorms NXT two-wheeled self-balancing robot (simply referred to in this study as NXT robot) has become a standard robot for developing several classes of humanoid robot
| [1] | P. Corke, “Robotics, Vision and Control Fundamental Algorithms in MATLAB®,” 2nd Edition, Springer Springer-Verlag, Heidelberg, 2017. |
| [2] | P. H. Petkov, T. N. Slavov and J. K. Kralev “Design of Embedded Robust Control Systems Using MATLAB®/Simulink®,” The Institution of Engineering and Technology, London, United Kingdom, 2018. |
| [3] | C. S. Chin, “Computer-Aided Control System Design: Practical Applications Using MATLAB® and Simulink®,” CRC Press - Taylor & Francis Group, Raton, USA, 2013. |
| [7] | A. A. Bobtsov, A. A. Pyrkin, S. A. Kolyubin, S. V. Shavetov, S. A. Chepinskiy, Y. A. Kapitanyuk, A. A. Kapitonov, V. M. Bardov, A. V. Titov and M. O. Surov, “Using of LEGO Mindstorms NXT Technology for Teaching of Basics of Adaptive Control Theory,” IFAC Proceedings Volumes, vol. 44, no. 1, pp. 9818-9823, 2011. |
| [8] | S. A. Fillippov, A. L. Fradkov, I. V. Ashikhmina and R. E. Seifullaev, “LEGO Mindstorms NXT Robot and Oscillators in Control Education,” IFAC Proceedings Volumes, vol. 43, no. 11, pp. 156-160, 2010. |
| [9] | B. A. Aleexeevich, A. K. Yuri, A. K. Alexander, A. K. Sergey, P. A. Alexandrovich, A. C. Sergey and V. S. Sergey, “LEGO Mindstorms NXT for Teaching the Principles of Adaptive Control to Students,” Sci. & Tech. J. of Inf. Tech., Mech. and Opt., vol. 355, no. 1(71), pp. 103-108, 2011. |
| [10] | M. Canale and S. Casale-Brunet, “A multidisciplinary approach for Model Predictive Control Education: A Lego Mindstorms NXT-based framework,” Int. J. of Cont., Aut. & Sys, vol. 12, no. 5, pp. 1030 - 1039, 2014. https://doi.org/10.1007/s12555-013-0282-7 |
[1-3, 7-10]
.
LEGO Mindstorms NXT Robot and Oscillators have been used to demonstrate the concept of adaptive control in education
| [7] | A. A. Bobtsov, A. A. Pyrkin, S. A. Kolyubin, S. V. Shavetov, S. A. Chepinskiy, Y. A. Kapitanyuk, A. A. Kapitonov, V. M. Bardov, A. V. Titov and M. O. Surov, “Using of LEGO Mindstorms NXT Technology for Teaching of Basics of Adaptive Control Theory,” IFAC Proceedings Volumes, vol. 44, no. 1, pp. 9818-9823, 2011. |
| [8] | S. A. Fillippov, A. L. Fradkov, I. V. Ashikhmina and R. E. Seifullaev, “LEGO Mindstorms NXT Robot and Oscillators in Control Education,” IFAC Proceedings Volumes, vol. 43, no. 11, pp. 156-160, 2010. |
| [9] | B. A. Aleexeevich, A. K. Yuri, A. K. Alexander, A. K. Sergey, P. A. Alexandrovich, A. C. Sergey and V. S. Sergey, “LEGO Mindstorms NXT for Teaching the Principles of Adaptive Control to Students,” Sci. & Tech. J. of Inf. Tech., Mech. and Opt., vol. 355, no. 1(71), pp. 103-108, 2011. |
| [10] | M. Canale and S. Casale-Brunet, “A multidisciplinary approach for Model Predictive Control Education: A Lego Mindstorms NXT-based framework,” Int. J. of Cont., Aut. & Sys, vol. 12, no. 5, pp. 1030 - 1039, 2014. https://doi.org/10.1007/s12555-013-0282-7 |
[7-10]
. Autonomous Mobile Robot has been implemented using LEGO EV3 integrated with Raspberry Pi which uses android-based vision control algorithms for human-machine interaction
| [11] | H. L. Araujo, J. G. Agudelo, R. C. Vidal, J. A. Uribe, J. F. Remolina, C. Serpa-Imbett, A. M. López and D. P. Guevara, “Autonomous Mobile Robot Implemented in LEGO EV3 Integrated with Raspberry Pi to Use Android-Based Vision Control Algorithms for Human-Machine Interaction,” Mach., vol. 10 no. 193, pp. 1-20, 2022. https://doi.org/10.3390/machines10030193 |
[11]
. Different variations and versions of adaptive control has been applied for the study and modeling of the LEGO Mindstorms NXT two-wheeled self-balancing robot based purely on linear models of the NXT robot as well as their implementation for different demonstrations and applications
| [2] | P. H. Petkov, T. N. Slavov and J. K. Kralev “Design of Embedded Robust Control Systems Using MATLAB®/Simulink®,” The Institution of Engineering and Technology, London, United Kingdom, 2018. |
| [12] | J. Y. Chen, T. F. Wu, P. S. Tsai and K. Y. Lian, “Indirect Adaptive Fuzzy Controller for LEGO Mindstorms NXT Two-Wheeled Robot,” App. Mech. & Mat., vols. 278-280, pp. 561-567, 2013, https://doi.org/10.4028/www.scientific.net/amm.278-280.561 |
| [13] | H C. Ащепкова “Development of adaptive control system of model of the robot-loader on the basis of Lego Mindstorms NXT,” Tech. Aud. & Prod. Res., vol. vol. 5(6), no. 25, pp. 45-48, 2015. https://doi.org/10.15587/2312-8372.2015.51215 |
[2, 12, 13]
. However, there is a strong differences between adaptive control based on model reference adaptive control (MRAC) and model predictive control (MPC)
| [14] | A. Mitov, J. Kralev, T. Slavov and I. Angelov, “Comparison between Model Predictive (MPC) and Model Reference Adaptive Controllers (MRAC) for Electrohydraulic Steering System Implemented as Real-Time Simulink® Program,” IOP Conf. Series: Mat. Sci. and Eng., vol. 1002, no. 012034, pp. 1-12, 2020. |
| [15] | V. A. Akpan and G. D. Hassapis, “Training dynamic feedforward neural networks for online nonlinear model identification and control applications,” Int. Rev. of Aut. Cont.: Theo. & App., vol. 4, no. 3, pp. 335 - 350, 2011. |
| [16] | V. A. Akpan and G. D. Hassapis, “Nonlinear model identification and adaptive model predictive control using neural networks,” ISA Trans.; vol. 5, no. 2, pp. 177-94, 2011. |
[14-16]
. Rather than the MRAC, the MPC strategy is adopted in this work.
Model predictive control (MPC) is a class of advanced control algorithms that utilize an explicit process model to predict the future response of the process and have been proven to be very successful in many industrial applications
| [16] | V. A. Akpan and G. D. Hassapis, “Nonlinear model identification and adaptive model predictive control using neural networks,” ISA Trans.; vol. 5, no. 2, pp. 177-94, 2011. |
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
| [18] | L. Kalra and C. Georgakis, “Effects of process nonlinearity on the performance of linear model predictive controllers for the environmentally safe operation of a fluid catalytic cracking unit,” Ind. Eng. Chem. Res, vol. 33, pp.3063-3069, 1994. |
| [19] | S. J. Qin and T. A. Badgwell, “A survey of model predictive control technology,” Cont. Eng. Pract., vol. 11, pp. 733 - 764, 2003. |
| [20] | V. A. Akpan, I. K. Samaras and G. D. Hassapis, “Implementation of Network Control System over a Service-Oriented-Architecture Computer Network Based on Device Profile for Web Services for Industrial Control Applications,” Int. J. of Cont. Sci. & Eng., vol. 12, no. 1, pp. 1-25, 2022. Available: http://article.sapub.org/10.5923.j.control.20221201.01.html |
| [21] | N. Khaled and B. Pattel, “Practical Design and Application of Model Predictive Control: MPC for MATLAB® and Simulink® Users,” Butterworth-Heinemann, Oxford, United Kingdom, 2018. |
| [22] | L. Grüne and J. Pannek, “Nonlinear Model Predictive Control: Theory and Algorithms,” Second Edition, Springer International Publishing, Switzerland, 2017. |
[16-22]
.
The design and implementation of online modeling and control algorithms for any class or type of robots with relatively short sampling time presents several challenges
| [1] | P. Corke, “Robotics, Vision and Control Fundamental Algorithms in MATLAB®,” 2nd Edition, Springer Springer-Verlag, Heidelberg, 2017. |
| [2] | P. H. Petkov, T. N. Slavov and J. K. Kralev “Design of Embedded Robust Control Systems Using MATLAB®/Simulink®,” The Institution of Engineering and Technology, London, United Kingdom, 2018. |
| [3] | C. S. Chin, “Computer-Aided Control System Design: Practical Applications Using MATLAB® and Simulink®,” CRC Press - Taylor & Francis Group, Raton, USA, 2013. |
[1-3]
. Rather than using linear model of the NXT robot, nonlinear modeling approach based on neural network is proposed in this work
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
[17]
. In fact, the algorithms obtained by MPC design techniques which are based on a linear mathematical model of the controlled process are not very efficient because these methods cannot guarantee stable control of the system outside the range of the model validity
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
| [18] | L. Kalra and C. Georgakis, “Effects of process nonlinearity on the performance of linear model predictive controllers for the environmentally safe operation of a fluid catalytic cracking unit,” Ind. Eng. Chem. Res, vol. 33, pp.3063-3069, 1994. |
| [19] | S. J. Qin and T. A. Badgwell, “A survey of model predictive control technology,” Cont. Eng. Pract., vol. 11, pp. 733 - 764, 2003. |
| [20] | V. A. Akpan, I. K. Samaras and G. D. Hassapis, “Implementation of Network Control System over a Service-Oriented-Architecture Computer Network Based on Device Profile for Web Services for Industrial Control Applications,” Int. J. of Cont. Sci. & Eng., vol. 12, no. 1, pp. 1-25, 2022. Available: http://article.sapub.org/10.5923.j.control.20221201.01.html |
| [21] | N. Khaled and B. Pattel, “Practical Design and Application of Model Predictive Control: MPC for MATLAB® and Simulink® Users,” Butterworth-Heinemann, Oxford, United Kingdom, 2018. |
| [22] | L. Grüne and J. Pannek, “Nonlinear Model Predictive Control: Theory and Algorithms,” Second Edition, Springer International Publishing, Switzerland, 2017. |
[17-22]
.
The present study focuses on the development of a neural network-based nonlinear modeling technique and a neural network-based nonlinear model adaptive predictive control approach for the online model identification and adaptive predictive control of the NXT robot.
The paper proposes an iterative technique for updating the Levenberg-Marquardt parameter which is a difficulty task for adapting and updating the NN parameters which are the weights and biases of the network.
The main challenge of the well-celebrated Levenberg-Marquardt algorithm (LMA) is the selection of the searching direction and adaptation parameters. Secondly, the implementation of the LMA for online model identification has faced challenges as it is a batch optimization. As a third challenge, the solution of the Levenberg-Marquardt based on the full-Newton nonlinear optimization (FNNO) for online applications have been limited due to its unguaranteed positive definiteness. Thus, by creating a continuously updated sliding stack window, the paper proposes an online implementation of the Levenberg-Marquardt algorithm. We refer to the proposed NN training algorithm as the online-window-approach based on modified Levenberg-Marquardt algorithm (OWA-MLMA) for training the NN model predictor.
The use of nonlinear NN model for nonlinear MPC has also been reported where the NN model is identified off-line and employed for online-line nonlinear MPC design based on the full-Newton method
| [23] | G. Colin, Y. Chamaillard, G. Bloch and G. Corde, “Neural control of fast nonlinear systems - Application to turbocharged SI engine with VCT,” IEEE Trans. Neu. Net., vol. 18, no. 4, pp. 1101 - 1114, Jul. 2007. |
| [24] | C. Lu and C. Tsai, “Adaptive predictive control with recurrent neural network for industrial process: An application to temperature control of a variable-frequency oil-cooling machine,” IEEE Trans. Ind. Elect., vol. 55, no. 3, pp. 1366-1375, Mar. 2008. |
[23, 24]
. The well-known problem with the full-Newton method is that the second-order Hessian matrix is not guaranteed to be positive definite in an open neighbourhood of a global minimum among other issues which have made this method unsuitable for online nonlinear adaptive model predictive control applications. This issue still remains open under current research and depends also on the accuracy of the online nonlinear model identification of the process
| [16] | V. A. Akpan and G. D. Hassapis, “Nonlinear model identification and adaptive model predictive control using neural networks,” ISA Trans.; vol. 5, no. 2, pp. 177-94, 2011. |
| [18] | L. Kalra and C. Georgakis, “Effects of process nonlinearity on the performance of linear model predictive controllers for the environmentally safe operation of a fluid catalytic cracking unit,” Ind. Eng. Chem. Res, vol. 33, pp.3063-3069, 1994. |
| [19] | S. J. Qin and T. A. Badgwell, “A survey of model predictive control technology,” Cont. Eng. Pract., vol. 11, pp. 733 - 764, 2003. |
[16, 18, 19]
.
This paper adopts the nonlinear adaptive model predictive control strategy which uses a nonlinear NN model for the controller design
| [16] | V. A. Akpan and G. D. Hassapis, “Nonlinear model identification and adaptive model predictive control using neural networks,” ISA Trans.; vol. 5, no. 2, pp. 177-94, 2011. |
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
[16, 17]
. The proposed control strategy is an online nonlinear optimization based on the full-Newton method using the modified Levenberg-Marquardt algorithm (MLMA)
| [15] | V. A. Akpan and G. D. Hassapis, “Training dynamic feedforward neural networks for online nonlinear model identification and control applications,” Int. Rev. of Aut. Cont.: Theo. & App., vol. 4, no. 3, pp. 335 - 350, 2011. |
| [16] | V. A. Akpan and G. D. Hassapis, “Nonlinear model identification and adaptive model predictive control using neural networks,” ISA Trans.; vol. 5, no. 2, pp. 177-94, 2011. |
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
[15-17]
. The proposed nonlinear adaptive predictive control (NAPC) scheme incorporates an iterative scheme for guaranteed positive definiteness of Hessian matrix and then applies another iterative technique to adjust and update the Levenberg-Marquardt parameter.
The paper is structured as follows. The development of the mathematical model, formulation of the control problem and the design of the desired reference trajectory for the NXT Robot is presented in Section 2. The neural network-based online-window-approach of the modified Levenberg-Marquardt algorithm (OWA-MLMA) based on approximate Gauss-Newton algorithm (AGNA) for training neural network for nonlinear model identification is formulated in Section 3. The summary of the incremental back-propagation algorithm (INCBPA) is also given in this Section. Then, Section 4 presents the complete formulation of the nonlinear adaptive predictive control (NAPC) algorithm based on MLMA using the full-Newton nonlinear optimization (FNNO-MLMA) and a PID control law for the NXT robot control. In Section 5, the off-line closed-loop implementation of the OWA-MLMA for NNARMAX model identification of the NXT robot is first presented with simulation results. Secondly, the identified NNARMAX model is then used to design the NAPC and PID controller for performance comparison. Lastly, the online closed-loop implementation of the OWA-MLMA and NAPC based on FNNO-MLMA and the simulation results are discussed and presented in this Section. Section 6 concludes the paper and highlights its major contributions and directions for further work.
Figure 1. Self-balancing two-wheeled LEGO Mindstorms NXTway-GS.
2. Development of the Mathematical Model, Formulation of the Control Problem, and the Design of the Desired Reference Trajectory for the NXT Robot
2.1. Mathematical Modeling of the NXT Robot as a Two-Wheel Inverted Pendulum
The two-wheeled NXT robot as an inverted pendulum shown in
Figure 1 can be considered as a two-wheel inverted pendulum model as shown in
Figure 2. The side and plane views of the two-wheel inverted pendulum model is shown in
Figure 3. The coordinate system of
Figure 3 can be used to formulate and derive the equations of motion for the two-wheel inverted pendulum as discussed in the next sub-section. Note that in
Figure 3,
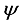
is the body pitch angle,
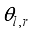
is the wheel angle (where
l and
r indicates left and right angles), and
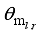
is the DC motor angle. The physical parameters of the NXT robot are defined in
Table 1.
Figure 2. The schematic of the two-wheeled inverted pendulum robot.
Figure 3. (a) Side view and (b) the plane view of the two-wheeled inverted pendulum.
2.1.1. Equations of Motion for the Two-Wheel Inverted Pendulum
We can now derive the equations of motion for the two-wheel inverted pendulum by the Lagrangian method based on the coordinate system in
Figure 3. If the direction of the two-wheel inverted pendulum is
x-axis positive direction at
t = 0, each coordinates are given as the following
| [2] | P. H. Petkov, T. N. Slavov and J. K. Kralev “Design of Embedded Robust Control Systems Using MATLAB®/Simulink®,” The Institution of Engineering and Technology, London, United Kingdom, 2018. |
| [25] | Y. Yamamoto, “NXTway-GS Model-Based Design: Control of self-balancing two-wheeled robot built with LEGO Mindstorms NXT,” Cybernet Systems Co. Limited, Revision 1.4, pp. 1 - 73, 2009. |
[2, 25]
:
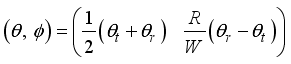 (1)
(1) 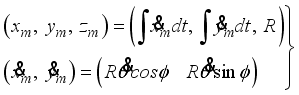 (2)
(2) 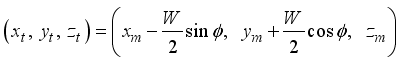 (3)
(3) Table 1. Physical parameters, numerical values and units for the self-balancing two-wheeled NXT robot.
S/N | Physical Parameters | Values | Units |
1 | Gravitational acceleration (g) | 9.810 | m.sec-2 |
2 | Wheel weight (m) | 0.030 | kg |
3 | Wheel radius (R) | 0.040 | m |
4 | Wheel inertia moment (JW) | mR2/2 | kg.m2 |
5 | Body weight (M) | 0.600 | kg |
6 | Body width (W) | 0.140 | m |
7 | Body depth (D) | 0.040 | m |
8 | Body height (H) | 0.144 | m |
9 | Distance of the centre of mass from the wheel axle (L) | H/2 | m |
10 | Body pitch inertia moment (Jψ) | ML2/3 | kg.m2 |
11 | Body yaw inertia moment (Jϕ) | M (W2 + D2)/12 | kg.m2 |
12 | DC motor inertia moment (Jm) | 1 x 10-5 | kg.m2 |
13 | DC motor resistance (Rm) | 6.690 | Ω |
14 | DC motor back EMF constant (Kb) | 0.468 | V.sec.rad-1 |
15 | DC motor torque constant (Kt) | 0.317 | Mn.A-1 |
16 | Gear ratio (n) | 1.000 | - |
17 | Friction coefficient between body and DC motor (fm) | 0.002 | - |
18 | Friction coefficient between wheel and floor (fW) | 0.000 | - |
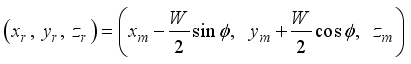 (4)
(4) 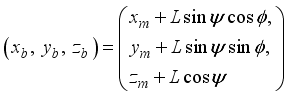 (5)
(5) The translational kinetic energy T1, the rotational kinetic energy T2 and the potential energy U are given respectively by:
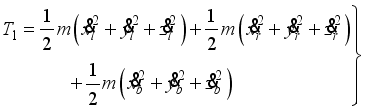 (6)
(6) 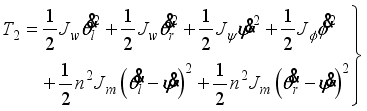 (7)
(7) 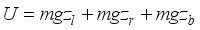 (8)
(8) The fifth and sixth terms in T2 are rotational kinetic energy of an armature in left and right DC motor. The Lagrangian (L) has the following expression:
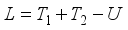 (9)
(9) where the generalized coordinates are defined with θ = average angle of left and right wheel, ψ = body pitch angle, and ϕ = body yaw angle.
The Lagrangian equations are the following:
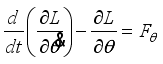 (10)
(10) 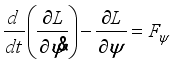 (11)
(11) 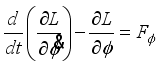 (12)
(12) Evaluation of (
10)-(
12) gives the following set of equations:
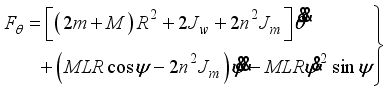 (13)
(13) 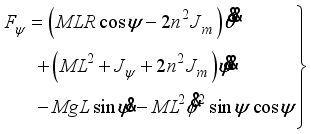 (14)
(14) 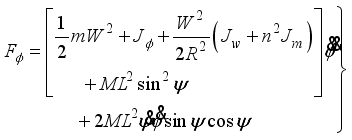 (15)
(15) In consideration of DC motor torque and viscous friction, the generalized forces are given as the following equations:
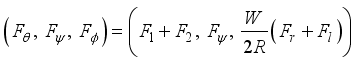 (16)
(16) where
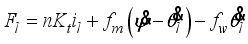 (17)
(17) 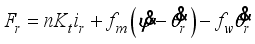 (18)
(18) 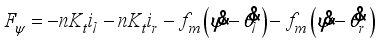 (19)
(19) and il,r is the DC motor current.
It should be noted that we cannot use the DC motor current directly in order to control the motor because it is based on PWM (voltage) control. Therefore, we need to evaluate the relation between current il,r and voltage vl,r using DC motor equations. If the friction inside the motor is negligible, the DC motor equation is generally as follows:
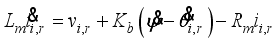 (20)
(20) Here we consider that the motor inductance is negligible and is approximated as zero. Therefore, the current becomes
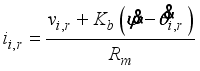 (21)
(21) From (
21), the generalized force can be expressed using the motor voltage as follows:
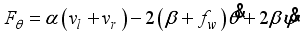 (22)
(22) 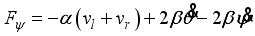 (23)
(23) 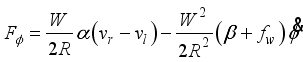 (24)
(24) where
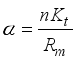
and
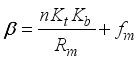 (25)
(25) 2.1.2. State Equations for the Two-Wheel Inverted Pendulum
We can now derive the state equations based on modern control theory by linearizing the equations of motion at a balance point of the robot based on the Taylor’s series
| [2] | P. H. Petkov, T. N. Slavov and J. K. Kralev “Design of Embedded Robust Control Systems Using MATLAB®/Simulink®,” The Institution of Engineering and Technology, London, United Kingdom, 2018. |
| [3] | C. S. Chin, “Computer-Aided Control System Design: Practical Applications Using MATLAB® and Simulink®,” CRC Press - Taylor & Francis Group, Raton, USA, 2013. |
| [4] | K. Ogata, “Modern Control Engineering,” Pearson Education, Inc., Prentice Hall, Upper Saddle River, New Jersey, USA, 2010. |
| [5] | W. S. Levine, “The Control Handbook: Control System Advanced Methods,” Second Edition, CRC Press - Taylor & Francis Group, New York, USA, 2011. |
| [6] | N. S. Nise, “Control Systems Engineering,” Seventh Edition, John Wiley & Sons Inc., California, USA. |
[2-6]
. It means that we consider the limit
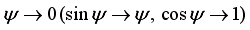
and neglect the second-order term like
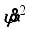
. The motion equations (
13-15) are approximated according to the following equations respectively:
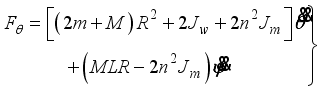 (26)
(26) 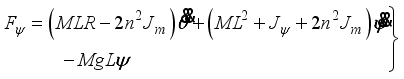 (27)
(27) 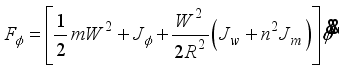 (28)
(28) Note that both (
26) and (
27) have
θ and
ψ, whereas (
28) has
ϕ only. These equations can be expressed in the following forms:
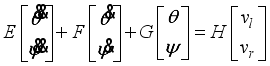 (29)
(29) where
and
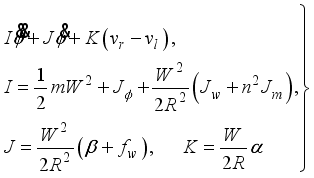 (30)
(30) Here we consider the variables x1, x2 as state variables and u as the input defined respectively by the following expressions:
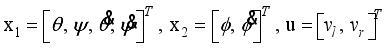 (31)
(31) Consequently, we can derive state equations for the two-wheeled inverted pendulum robotic system from (
29) and (
30) as follows:
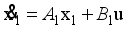 (32)
(32) 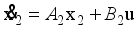 (33)
(33) where
 (34)
(34) 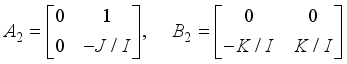 (35)
(35) and
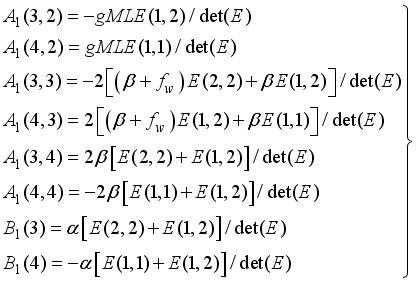 (36)
(36) with
2.2. Control Problem Formulation for the Self-Balancing Two-Wheel NXT Robot as an Inverted Pendulum
The characteristics of the self-balancing two-wheel NXT robot as a control system are described as follows.
2.2.1. Inputs and Outputs
The input to the actuator is PWM duty of the left and right DC motor even though input u in (
31) is voltage. The outputs from sensors are the DC motor angle
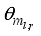
and the body pitch angular velocity
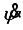
. It is easy to evaluate
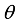
and
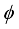
by using
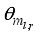
. There are two methods to evaluate
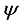
by using
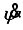
, namely:
1). Derive
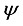
by integrating the angular speed numerically and
2). Estimate
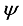
by using an observer based on modern control theory. In this study, we use the second method in the following for the controller design chiefly because of easy stability establishment.
2.2.2. Stability of the NXTway-GS Robot
It is easy to understand that NXT robot balancing position is not stable. We have to move NXT robot in the same direction of body pitch angle to keep balancing. Modern control theory gives many techniques to stabilize an unstable system.
Equation (
29) is a similar equation as mass-spring-damper system.
Figure 4 shows an equivalent system of two-wheeled inverted pendulum interpreted as mass-spring-damper system. We find out that we can make the two-wheeled inverted pendulum stable by adjusting spring constants and damper friction constants in
Figure 4. The Simulink model of the self-balancing two-wheel NXT robot is shown in
Figure 5.
Figure 4. Equivalent mass-spring-damper system for one side of the two-wheeled inverted pendulum of the NXT robot.
Figure 5. Simulink model of the self-balancing two-wheel NXT robot.
2.2.3. Simulation of the MATLAB/Simulink Model of the NXT Robot for Data Generation
The NXT robot uses the model reference feature as the controller and plant parts that have different Simulink model files. This modeling approach allows a parallel development process for controller design and physical plant design. Simulink buses and bus objects are used to keep the interface between the controller model and plant model. The MATLAB/Simulink, from the MathWorks
| [26] | The MathWorks Inc., MATLAB® & Simulink® 2025, Natick, USA. Available: www.mathworks.com |
[26]
, is used to program, model and simulate the mathematical model of the self-balancing two-wheel NXT robot. The data generated from the simulation MATLAB/Simulink model of the self-balancing two-wheel NXT robot are shown in
Figure 6(a) and 6(b) for 250,000 data samples. The inputs to the NXT robot are the voltages to the Left and Right wheels of the self-balancing two-wheel NXT robot a shown in
Figure 6(a) and 6(b) respectively. The outputs of the NXT robot are the angles of rotation of the Left and Right wheels of the self-balancing two-wheel NXT robot as shown in
Figure 7(a) and 7(b) respectively.
Figure 6. The NXT robot motor input voltage (V): (a) Left wheel motor and (b) Right wheel motor.
Figure 7. The NXT robot output wheel rotation in degrees (°): (a) Left wheel rotation and (b) Right wheel rotation.
2.3. Desired NXT Robot Trajectory Design
2.3.1. Operation of the Robot Based on the Controlled Variable Based on the Manipulated Variables
The typical operation of the robot based on each of the controlled variables (i.e., the angle of rotation of the right and left wheels as the outputs) of the NXT Robot based on the manipulated variables (i.e., the input voltages to left and right wheels as the inputs) are described as follows:
1) For the robot to achieve forward movement, right and left wheel motor voltages should be kept high (i.e., +5 V). The robot wheel angle of rotation should be maintained at 90°.
2) To achieve a backward movement of the robot, both the right and left wheel motor voltages should be reversed (i.e., -5 V). The robot wheel angle of rotation should be maintained at 90°.
3) For the robot to turn to the right direction, the right wheel motor voltage should be stationary at logic low (i.e., stationary at 0 V) while the left wheel motor voltage should be maintained at logic high (i.e., +5 V). This will keep the robot left wheel moving while the robot turns right until the desired angle of rotation is achieved (i.e., from 90° to 180°, 270°, 360° and possibly back to 90° as the case may be).
4) For the robot to turn to the left direction, the left wheel motor voltage should be stationary at logic low (i.e., stationary at 0 V) while the right wheel motor voltage should be maintained at logic high (i.e., +5 V). This will keep the robot right wheel moving while the robot turns left until the desired angle of rotation is achieved (i.e., from 90° to -180°, -270°, -360° and possibly back to 90° as the case may be).
2.3.2. Design of the Desired Reference Trajectory for the Robot Based on the Controlled Variables (CV) and the Manipulated Variables (MV)
The NXT-robot wheels have several features for achieving its movement, manipulative and functional characteristics. In the following discussion stationary is logic 0 (i.e. 0 V), logic low is -5 V and logic high is +5 V. Each sampling instant is 20 seconds which corresponds to to the sampling time of the robot as arbitrarily considered in this work.
At the first sampling instant both the left wheel and the right wheel of the NXT robot are stationary for a period of 20 seconds.
At second sampling instant, the left wheel and the right wheel are both at logic high and the NXT robot moves forward.
At the third sampling instant, the left wheel is at logic high while the right wheel is at logic low, then the NXT robot turns to the right wing.
At the fourth sampling instant, the left wheel is stationary and the right wheel is at logic high, the NXT robot is turning to the left wing.
At the fifth sampling instant, the left wheel is at logic low, while the right is also at logic low, the NXT robot moves backward.
At the sixth sampling instant, the left wheel is stationary while the right wheel is at logic high, then the NXT robot turns to the left wing.
At the seventh sampling instant, the left wheel is at logic high, while the right wheel is stationary, then theNXT robot then rotates to the right wing.
At the eighth sampling instant, both the wheels are at logic high; this makes the NXT robot to move forward again.
At the ninth sampling instant, the left wheel is stationary while the right wheel is at logic high, then the NXT robot rotates to the left.
At the tenth sampling instant, the left wheel is at logic high while the right wheel is stationary, and this forces the NXT robot to rotate to the right wing.
At the eleventh sampling instant, the left wheel is at logic low, while the right wheel is also at logic low, then the NXT robot movement is reversed and the robot moves backward.
At the twelfth sampling instant, the left wheel is at logic high, while the right wheel is stationary, then the NXT-robot rotates to the right wing.
At the thirteenth sampling instant, the left wheel is stationary, while the right wheel is at logic high, this makes the NXT robot to rotate to the left.
Finally, at the fourteenth sampling instant, the left wheel of the NXT robot is at logic low while the right wheel is at stationary, which forces the NXT robot to come to rest.
On the basis of the prescribed operation of the NXT robot based on the controlled variables (outputs) based on the manipulated variables (inputs) described in sub-section 2.3.1 and the desired reference trajectory design for the NXT robot based on the controlled variables and the manipulated variables discussed in Sub-Section 2.3.2 above, the desired reference trajectory for the NXT robot used in this work is constructed as shown in
Figure 8.
Figure 8. The desired reference trajectories for the NXT Robot.
3. Formulation of the OWA-MLMA Based on AGNA for Training NNARMAX Model Predictor
3.1. The OWA-MLMA Based on AGNA
In this section we first introduce the system description. In the next sub-section, we introduce the basic MLP NN and its extension to the series-parallel structure of NNARMAX model identification. Then in the last sub-section, we present the OWA-MLMA for training the NN to adjust and update the NN parameters (i.e. weights and biases) for NNARMAX model identification.
3.1.1. General System Description
The method of representing dynamical systems by vector difference or differential equations is well established in systems
| [27] | L. Lung, “System Identification: Theory for the User,” 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 1999. |
[27]
and control
| [2] | P. H. Petkov, T. N. Slavov and J. K. Kralev “Design of Embedded Robust Control Systems Using MATLAB®/Simulink®,” The Institution of Engineering and Technology, London, United Kingdom, 2018. |
| [16] | V. A. Akpan and G. D. Hassapis, “Nonlinear model identification and adaptive model predictive control using neural networks,” ISA Trans.; vol. 5, no. 2, pp. 177-94, 2011. |
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
| [18] | L. Kalra and C. Georgakis, “Effects of process nonlinearity on the performance of linear model predictive controllers for the environmentally safe operation of a fluid catalytic cracking unit,” Ind. Eng. Chem. Res, vol. 33, pp.3063-3069, 1994. |
| [19] | S. J. Qin and T. A. Badgwell, “A survey of model predictive control technology,” Cont. Eng. Pract., vol. 11, pp. 733 - 764, 2003. |
| [20] | V. A. Akpan, I. K. Samaras and G. D. Hassapis, “Implementation of Network Control System over a Service-Oriented-Architecture Computer Network Based on Device Profile for Web Services for Industrial Control Applications,” Int. J. of Cont. Sci. & Eng., vol. 12, no. 1, pp. 1-25, 2022. Available: http://article.sapub.org/10.5923.j.control.20221201.01.html |
| [21] | N. Khaled and B. Pattel, “Practical Design and Application of Model Predictive Control: MPC for MATLAB® and Simulink® Users,” Butterworth-Heinemann, Oxford, United Kingdom, 2018. |
| [22] | L. Grüne and J. Pannek, “Nonlinear Model Predictive Control: Theory and Algorithms,” Second Edition, Springer International Publishing, Switzerland, 2017. |
[2, 16-22]
theories. Consider that the
ith output
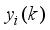
of a discrete-time nonlinear
m-input
n-output multivariable system at time instant
k responding to the
lth input
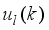
can be described by the following Nonlinear AutoRegressive Moving Average with eXogeneous input (NARMAX) model:
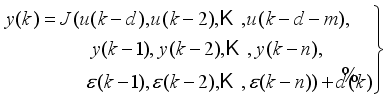 (37)
(37) where
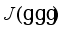
is a nonlinear function of its input arguments assumed to be differentiable,
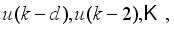
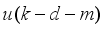
,
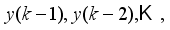
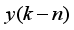
and
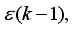
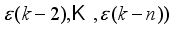
are the vectors of the past input, past output and past prediction error values respectively while
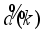
are the disturbances and
d is the system delay. Assuming that the input-output data pair
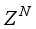
of the system taken over
NT period of time is available
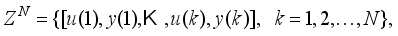 (38)
(38) where
N is the number of data pair and
T the sampling time. Equation (
37) can be expressed in a more compact form as
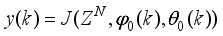 (39)
(39) where
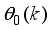
is a known vector of appropriate dimension that defines the parameters of the system and
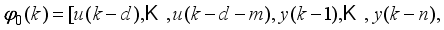
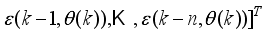
is the state (regression) vector at time
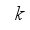
.
To set up a model identification problem, given (
38),
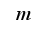
,
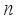
, with an initial small random value of
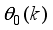
; at time
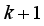
we can construct a predictor
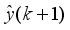
that will produce the
a priori predictor estimate of (
39)
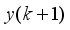
based on the state of the system
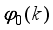
at time
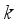
can be define as
where
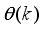
is an unknown adjustable parameter vector of appropriate dimension and the regression (state) vector
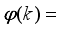
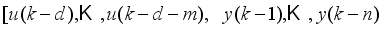
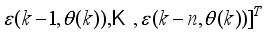
. Thus, at time
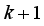
a new value of
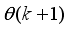
will be known and the
a posteriori predictor estimate can be computed as
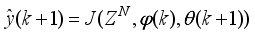 (40)
(40) where the predictor output
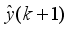
is compared to the system output
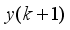
and the error
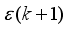
between the two outputs is minimized and used to adjust and update
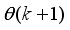
such that
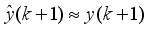
. It is evident that the predictor output depends on
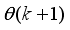
. For notational convenience, we define the error here as:
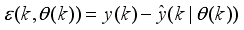 (41)
(41) where
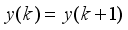
,
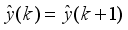
and
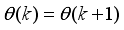
are the true system output, network predicted output and the adjustable parameters of the network. Thus, the determination and adjustment of
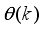
becomes an unconstrained nonlinear minimization problem defined here as:
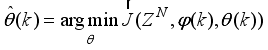 (42)
(42) where
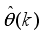
is the value of
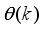
that minimizes (
42) and
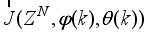
is formulated as a total square error (TSE) type cost function given as:
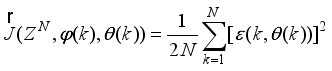 (43)
(43) Several techniques for solving (
42) exist in literature
| [27] | L. Lung, “System Identification: Theory for the User,” 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 1999. |
| [28] | R. Chiong, “Intelligent Systems for Automated Learning and Application: Emerging Trends and Application,” Hershey PA, USA: Information Science Reference, 2010, ch. 4, pp. 204 - 316. |
| [29] | J. Wu, “Multilayer pottsperceptrons with Levenberg-Marquardt learning,” IEEE Trans. Neu. Net., vol. 19, no. 12, pp. 2032-2043, Dec. 2008. |
[27-29]
. Following the discussion in the Section I, the NN technique is proposed in this paper for solving (
42) based on its nonlinear model approximation capabilities
| [16] | V. A. Akpan and G. D. Hassapis, “Nonlinear model identification and adaptive model predictive control using neural networks,” ISA Trans.; vol. 5, no. 2, pp. 177-94, 2011. |
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
| [20] | V. A. Akpan, I. K. Samaras and G. D. Hassapis, “Implementation of Network Control System over a Service-Oriented-Architecture Computer Network Based on Device Profile for Web Services for Industrial Control Applications,” Int. J. of Cont. Sci. & Eng., vol. 12, no. 1, pp. 1-25, 2022. Available: http://article.sapub.org/10.5923.j.control.20221201.01.html |
| [30] | V. A. Akpan and R. A. O. Osakwe, “Multivariable NNARMAX Model Identification of an AS-WWTP Using ARLS (Part 1: Dynamic Modeling of the Biological Reactors),” American J. of Int. Sys., vol. 4, no. 2, pp. 43 - 72, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140402.03.pdf |
| [31] | V. A. Akpan and R. A. O. Osakwe, “Multivariable NNARMAX Model Identification of an AS-WWTP Using ARLS (Part 2: Dynamic Modeling of the Secondary Settler and Clarifier),” American J. of Int. Sys., vol. 4, no. 3, pp. 77 - 106, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140403.02.pdf |
| [32] | V. A. Akpan and R. A. O. Osakwe, “Online Prediction of Influent Characteristics for Wastewater Treatment Plants Management Using Adaptive Recursive NNARMAX Model,” American J. of Int. Sys., vol. 4, no. 3, pp. 107 - 130, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140403.03.pdf |
[16, 17, 20, 30-32].
3.1.2. The Neural Network Identification Model
The proposed NN model identification scheme is based on the series-parallel structure shown in
Figure 9 where the system is in parallel with the NN identification model (in the dashed box) and
TDL denotes tapped delay line memory. The NN identification model consists of a training algorithm and the NN model. The inputs to the NN model, via an
m-TDL and
n-TDL, are the past
m-inputs and
n-outputs contained in
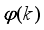
which is obtained from
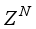
defined in (
38).
The NN identification model of
Figure 10 has a recurrent architecture since it contains feedbacks form the output of the system rather than the output of the NN model
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
[17]
. This is the so-called teacher forcing method where the network output is forced to follow the system outputs which leads to faster training in real-time
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
[17]
. With this method, the NNARMAX model can be trained as a FNN.
Figure 9. The NXT robot NNARMAX model identification scheme using OWA-MLMA training algorithm.
Figure 10. Architecture of the dynamic feedforward NN (DFNN) model.
The NNARMAX model architecture proposed here is a MLP NN with two-layers (one hidden and one output layer) shown in
Figure 10. To obtain the mathematical description of
Figure 10,
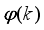
in (
42) is decomposed into the past input, past output and past prediction error parts
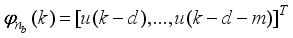
,
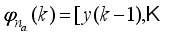
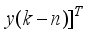
and
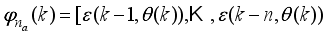
respectively. The outputs of the NN model of
Figure 10 can be expressed in terms of the network parameters as:
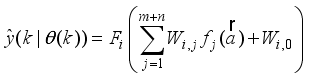 (44)
(44) where
j is the number of hidden neurons;
and
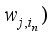
and
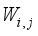
are the hidden and output weights respectively;
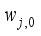
and
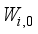
are the hidden and output biases;
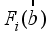
is a linear activation function for the output layer and
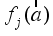
is an hyperbolic tangent activation function for the hidden layer given here as:
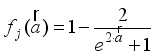 (45)
(45) Bias is interpreted as a weight acting on the input clamped to 1. Here, the network weights and biases constitute
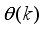
.
Regularization can reduce the modeling errors inherent in dynamical systems modeling while improving the robustness and performance of second-order training algorithm for finite data set
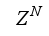
| [27] | L. Lung, “System Identification: Theory for the User,” 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 1999. |
| [28] | R. Chiong, “Intelligent Systems for Automated Learning and Application: Emerging Trends and Application,” Hershey PA, USA: Information Science Reference, 2010, ch. 4, pp. 204 - 316. |
| [29] | J. Wu, “Multilayer pottsperceptrons with Levenberg-Marquardt learning,” IEEE Trans. Neu. Net., vol. 19, no. 12, pp. 2032-2043, Dec. 2008. |
[27-29]
. One common method of implementing regularization is by weight decay
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
| [27] | L. Lung, “System Identification: Theory for the User,” 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 1999. |
| [30] | V. A. Akpan and R. A. O. Osakwe, “Multivariable NNARMAX Model Identification of an AS-WWTP Using ARLS (Part 1: Dynamic Modeling of the Biological Reactors),” American J. of Int. Sys., vol. 4, no. 2, pp. 43 - 72, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140402.03.pdf |
| [31] | V. A. Akpan and R. A. O. Osakwe, “Multivariable NNARMAX Model Identification of an AS-WWTP Using ARLS (Part 2: Dynamic Modeling of the Secondary Settler and Clarifier),” American J. of Int. Sys., vol. 4, no. 3, pp. 77 - 106, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140403.02.pdf |
| [32] | V. A. Akpan and R. A. O. Osakwe, “Online Prediction of Influent Characteristics for Wastewater Treatment Plants Management Using Adaptive Recursive NNARMAX Model,” American J. of Int. Sys., vol. 4, no. 3, pp. 107 - 130, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140403.03.pdf |
[17, 27, 30-32]
. According to this method, the cost function (
43) is augmented with a weight decay term defined as
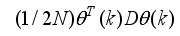
; where
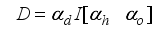
,
is an identity matrix,
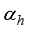
and
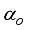
are the weight decay values for the input-to-hidden and hidden-to-output layers respectively. Using (
44), the regularized criterion from (
43) becomes:
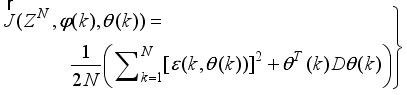 (46)
(46) and the minimization problem (
42) is re-written as
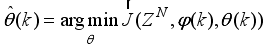 (47)
(47) Because NN training is a data-driven method, it should be noted that there are several ways on how
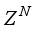
can be presented to the training algorithm at each time step. The most popular way being the batch (off-line) mode where all the data set
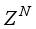
is evaluated at each time step and the recursive (online) mode where each data pair of
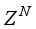
is evaluated at each time step.
This paper uses a different approach based on a first-in first out sliding stack OWA which store a short history of the input-output data. The stack discards the oldest data as new input-output data pair are progressively added to
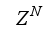
at each sampling time step and all the data are evaluated in batch mode at each sampling time step.
3.1.3. Approximate Gauss-Newton Algorithm (AGNA)
The minimization of (
47) is based on an iterative procedure which starts with a randomly initial
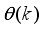
and updates

iteratively according to the following typical updating rule:
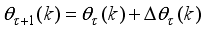 (48)
(48) where
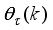
denotes
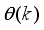
at the current iteration
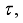
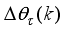
is the searching direction,
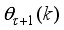
is the global minimum and
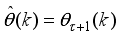
if certain stopping criteria are satisfied.
The most commonly used method for updating
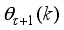
is the back-propagation algorithm (BPA)
| [33] | D. E. Rumelhart, G. E. Hinton and R. J. Williams, “Learning representations by back-propagating errors,” Nat., vol. 323, pp. 533-536, 1986. |
| [34] | P. J. Werbos, “Backpropagation through time: What it does and how to do it,” In Proc. IEEE, vol. 78, no. 10, pp. 1550 - 1560, Oct. 1990. |
[33, 34]
. This algorithm uses the gradient method
| [28] | R. Chiong, “Intelligent Systems for Automated Learning and Application: Emerging Trends and Application,” Hershey PA, USA: Information Science Reference, 2010, ch. 4, pp. 204 - 316. |
| [35] | J. E. Dennis and R. B. Schnabel, “Numerical Methods for Unconstrained Optimization and Nonlinear Equations,” Englewood Cliffs, NJ: Prentice-Hall, 1996. |
| [36] | M. T. Hagan and M. B. Menhaj, “Training feedforward network with the Marquardt algorithm,” IEEE Trans. Neu. Net., vol. 5, no. 6, pp. 989-993, Nov. 1994. |
| [37] | R. Fletcher, “Practical Methods of Optimization,” 2nd ed., Chichester: Wiley & Sons, 1987. |
[28, 35-37]
and set the
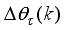
directly proportional to the negative of the gradient of (
46) evaluated at
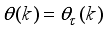
. Using (
46) and (
48), the basic BP algorithm can be stated as:
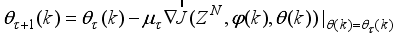 (49)
(49) where
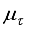
is the step size and

is the gradient NN training using the BPA has been reported to be characterized by poor performance
| [28] | R. Chiong, “Intelligent Systems for Automated Learning and Application: Emerging Trends and Application,” Hershey PA, USA: Information Science Reference, 2010, ch. 4, pp. 204 - 316. |
| [29] | J. Wu, “Multilayer pottsperceptrons with Levenberg-Marquardt learning,” IEEE Trans. Neu. Net., vol. 19, no. 12, pp. 2032-2043, Dec. 2008. |
| [36] | M. T. Hagan and M. B. Menhaj, “Training feedforward network with the Marquardt algorithm,” IEEE Trans. Neu. Net., vol. 5, no. 6, pp. 989-993, Nov. 1994. |
[28, 29, 36]
. To improve the performance of the BP algorithm, the Gauss-Newton method has been widely used as a starting point for this purpose.
The AGNA uses the linear approximation error
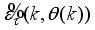
to the error
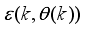
in (
45) expressed as:
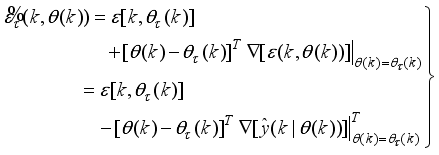 (50)
(50) to obtain (
46) as a quadratic criterion
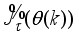
given as
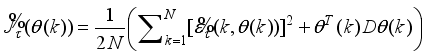 (51)
(51) where
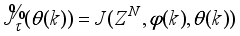
from now on shall be used for convenience. Note that Equation (
17) can also be expressed as
| [15] | V. A. Akpan and G. D. Hassapis, “Training dynamic feedforward neural networks for online nonlinear model identification and control applications,” Int. Rev. of Aut. Cont.: Theo. & App., vol. 4, no. 3, pp. 335 - 350, 2011. |
| [16] | V. A. Akpan and G. D. Hassapis, “Nonlinear model identification and adaptive model predictive control using neural networks,” ISA Trans.; vol. 5, no. 2, pp. 177-94, 2011. |
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
[15-17]
:
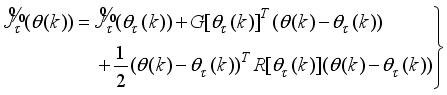 (52)
(52) where
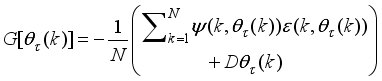 (53)
(53) and
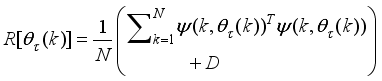 (54)
(54) where
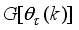
and
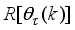
are the gradient and exact Gauss-Newton Hessian matrices respectively, and
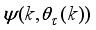
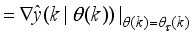
denotes the derivative of the network output with respect to
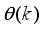
evaluated at
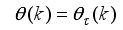
. By substituting
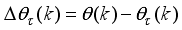
into (
52) and setting its derivative to zero as follows:
we obtain the AGNA searching direction given as
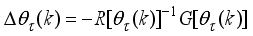 (55)
(55) Using (
49), the AGNA can be stated as:
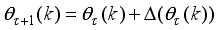 (56)
(56) where
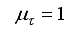
. Equation (
54) is guaranteed to be positive definite since it is based a second-order approximation of (
47) which is well-known to be positive definite
| [35] | J. E. Dennis and R. B. Schnabel, “Numerical Methods for Unconstrained Optimization and Nonlinear Equations,” Englewood Cliffs, NJ: Prentice-Hall, 1996. |
[35]
. The major problems with the Gauss-Newton method are slow convergence due to
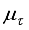
especially when
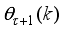
is far from
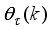
and (
53) can sometimes be ill-conditioned. In the next sub-section, we utilize (
56) to formulate the proposed OWA-MLMA based on AGNA which addresses the above issues dynamically.
3.1.4. The OWA-MLMA Based on AGNA
The Levenberg-Marquardt’s modification to (
55) is the introduction of a nonnegative parameter
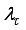
to the diagonal of
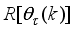
with a new updating rule given as
| [35] | J. E. Dennis and R. B. Schnabel, “Numerical Methods for Unconstrained Optimization and Nonlinear Equations,” Englewood Cliffs, NJ: Prentice-Hall, 1996. |
| [36] | M. T. Hagan and M. B. Menhaj, “Training feedforward network with the Marquardt algorithm,” IEEE Trans. Neu. Net., vol. 5, no. 6, pp. 989-993, Nov. 1994. |
| [37] | R. Fletcher, “Practical Methods of Optimization,” 2nd ed., Chichester: Wiley & Sons, 1987. |
[35-37]
:
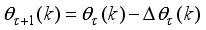 (57)
(57) where
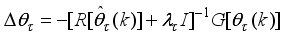 (58)
(58) is the searching direction and I is a diagonal matrix.
The parameter
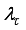
characterizes a hybrid of searching directions and has several effects
| [35] | J. E. Dennis and R. B. Schnabel, “Numerical Methods for Unconstrained Optimization and Nonlinear Equations,” Englewood Cliffs, NJ: Prentice-Hall, 1996. |
| [36] | M. T. Hagan and M. B. Menhaj, “Training feedforward network with the Marquardt algorithm,” IEEE Trans. Neu. Net., vol. 5, no. 6, pp. 989-993, Nov. 1994. |
| [37] | R. Fletcher, “Practical Methods of Optimization,” 2nd ed., Chichester: Wiley & Sons, 1987. |
[35-37]
:
1). for large values of
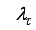
, Equation (
57) reduces to the steepest descent algorithm (with step
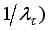
which requires a descend search method; and
2). for small values of
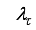
, Equation (
57) reduces to Gauss-Newton algorithm (with step given by (
56)).
The convergence of (
57) may be slowed if the magnitude of
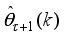
is large
| [28] | R. Chiong, “Intelligent Systems for Automated Learning and Application: Emerging Trends and Application,” Hershey PA, USA: Information Science Reference, 2010, ch. 4, pp. 204 - 316. |
| [29] | J. Wu, “Multilayer pottsperceptrons with Levenberg-Marquardt learning,” IEEE Trans. Neu. Net., vol. 19, no. 12, pp. 2032-2043, Dec. 2008. |
| [36] | M. T. Hagan and M. B. Menhaj, “Training feedforward network with the Marquardt algorithm,” IEEE Trans. Neu. Net., vol. 5, no. 6, pp. 989-993, Nov. 1994. |
[28, 29, 36]
. Here, we modify (
58) by introducing a scaling matrix
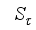
, so that (
58) becomes
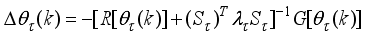 (59)
(59) where the scaling matrix
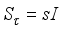
is adjusted simultaneously with
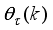
in the search for
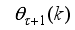
by (
57),
s is the scaling parameter, and
I is an identity. The solution to (
57) using (
59) based on the trust region method
| [35] | J. E. Dennis and R. B. Schnabel, “Numerical Methods for Unconstrained Optimization and Nonlinear Equations,” Englewood Cliffs, NJ: Prentice-Hall, 1996. |
| [36] | M. T. Hagan and M. B. Menhaj, “Training feedforward network with the Marquardt algorithm,” IEEE Trans. Neu. Net., vol. 5, no. 6, pp. 989-993, Nov. 1994. |
[35, 36]
can then be stated as a constrained minimization problem defined by:
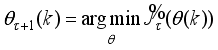 (60)
(60) subject to
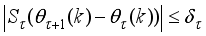
.
where
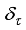
is the trust region radius within which
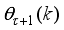
can be found. A difficulty with the Levenberg-Marquardt method is in selecting and adjusting the parameter
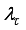
as well as how
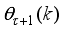
should be updated. The choice for the proper selection of
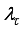
has led to the formulation of several algorithms
| [28] | R. Chiong, “Intelligent Systems for Automated Learning and Application: Emerging Trends and Application,” Hershey PA, USA: Information Science Reference, 2010, ch. 4, pp. 204 - 316. |
| [29] | J. Wu, “Multilayer pottsperceptrons with Levenberg-Marquardt learning,” IEEE Trans. Neu. Net., vol. 19, no. 12, pp. 2032-2043, Dec. 2008. |
| [35] | J. E. Dennis and R. B. Schnabel, “Numerical Methods for Unconstrained Optimization and Nonlinear Equations,” Englewood Cliffs, NJ: Prentice-Hall, 1996. |
| [36] | M. T. Hagan and M. B. Menhaj, “Training feedforward network with the Marquardt algorithm,” IEEE Trans. Neu. Net., vol. 5, no. 6, pp. 989-993, Nov. 1994. |
| [37] | R. Fletcher, “Practical Methods of Optimization,” 2nd ed., Chichester: Wiley & Sons, 1987. |
[28, 29, 35-37]
.
The approach in this paper builds on the indirect method described in
| [37] | R. Fletcher, “Practical Methods of Optimization,” 2nd ed., Chichester: Wiley & Sons, 1987. |
[37]
which has been shown in
| [15] | V. A. Akpan and G. D. Hassapis, “Training dynamic feedforward neural networks for online nonlinear model identification and control applications,” Int. Rev. of Aut. Cont.: Theo. & App., vol. 4, no. 3, pp. 335 - 350, 2011. |
| [16] | V. A. Akpan and G. D. Hassapis, “Nonlinear model identification and adaptive model predictive control using neural networks,” ISA Trans.; vol. 5, no. 2, pp. 177-94, 2011. |
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
[15-17]
to outperform the original Levenberg-Marquardt algorithm
| [38] | K. Levenberg, “A method for the Solution of Certain Non-Linear,” Problems in Least Squares”, Quart. ofAppl Math., vol. 2, no. 2, pp. 164 - 168, 1944. https://doi.org/10.1090/qam/10666 |
| [39] | D. W. Marquardt, “An algorithm for least-squares estimation of nonlinear parameters,” J. Soc. for Ind. & Appl. Math., vol. 11, no. 2, pp. 431-441, 1963. https://doi.org/10.1137/0111030 |
[38, 39]
. According to this method
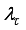
is adjusted based on the ratio
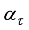
between the actual reduction
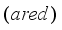
and theoretical predicted decrease
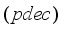
subject to the constraint in (
60) stated here as:
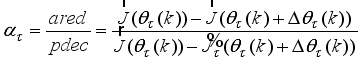 (61)
(61) where
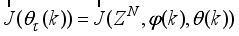
in (
46) for convenience.
Thus, we summarize the OWA-MLMA based on AGNA for training NN in a stepwise procedure as follows:
1) Specify
τ,
 D
D,
and
m and
n for
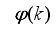
.
2) Initialize
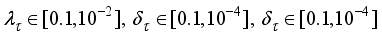
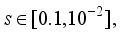
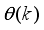
and evaluate
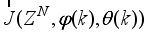
in (
46).
3) While
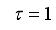
, compute
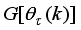
and
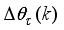
using (
53) and (
58) respectively.
4) Evaluate the ratio
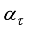
in (
61).
5) Update
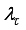
according to the following conditions on
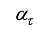
:
If
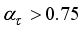
, then
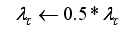
and go to
Step6).
If
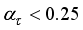
, then
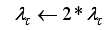
and go to
Step 6).
6) If
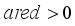
, then
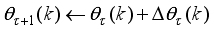
subject to (
53)
Set
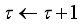
and
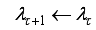
.
7) If
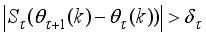
or
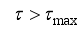
or
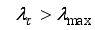
(number of iterations); go to
Step 8), else go to
Step 3).
8) Accept
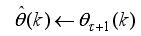
and terminate.
3.2. The Incremental or Online Back-Propagation Algorithm (INCBPA)
In order to investigate the performance of the OWA-MLMA based on AGNA, the so-called incremental back-propagation algorithm (INCBPA) is used for this purpose. The INCBPA (or online recursive version of the BPA) was originally proposed by
| [40] | J. Hertz, A. Krough and R. G. Palmer, “An Introduction to the Theory of Neural Computation,” Lecture Notes, vol. 1, Redwood City, California: Addison-Wesley, 1991. |
[40]
which has been modified in
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
[17]
and used in this paper. The incremental back-propagation (INCBP) algorithm is given as:
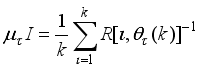 (62)
(62) where
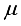
is the step size and
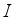
is an identity matrix of appropriate dimension. Next, the basic back-propagation given as
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
| [33] | D. E. Rumelhart, G. E. Hinton and R. J. Williams, “Learning representations by back-propagating errors,” Nat., vol. 323, pp. 533-536, 1986. |
| [34] | P. J. Werbos, “Backpropagation through time: What it does and how to do it,” In Proc. IEEE, vol. 78, no. 10, pp. 1550 - 1560, Oct. 1990. |
[17, 33, 34]
:
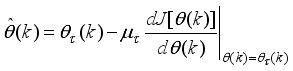 (63)
(63) is used to update the algorithm of (
62). Finally, all that is required is to specify a suitable step size
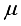
and carry out the recursive computation of the gradient given by (
63).
4. Formulation of the NAPC Based on FNNO-MLMA
4.1. NAPC Based on FNNO-MLMA
4.1.1. Formulation of the MPC Control Problem and the MPC Strategy
The block diagram of the NAPC based on FNNO-MLMA control with OWA-MLMA based on AGNA is shown in
Figure 11; where
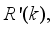
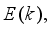
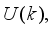
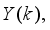
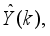
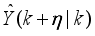
,
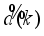
and
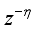
are the desired reference signal, prediction error, control input, system output,
η step-delay prediction model output,
η step-ahead predicted output, noise/input disturbances and
ηstep-delay operator respectively and
k is the number of samples based on the new measurement data sample.
Figure 11. The NAPC-based FNNO-MLMA control scheme for the NXT robot control with the OWA-MLMA based on AGNA for training the NNARMAX model predictor.
As in basic MBPC scheme
| [16] | V. A. Akpan and G. D. Hassapis, “Nonlinear model identification and adaptive model predictive control using neural networks,” ISA Trans.; vol. 5, no. 2, pp. 177-94, 2011. |
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
| [20] | V. A. Akpan, I. K. Samaras and G. D. Hassapis, “Implementation of Network Control System over a Service-Oriented-Architecture Computer Network Based on Device Profile for Web Services for Industrial Control Applications,” Int. J. of Cont. Sci. & Eng., vol. 12, no. 1, pp. 1-25, 2022. Available: http://article.sapub.org/10.5923.j.control.20221201.01.html |
[16, 17, 20]
, the prediction errors
E (k) between the process model and the prediction model are compensated by filtering the reference signal using a first-order low-pass digital filter defined here as:
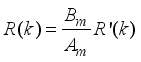 (64)
(64) where
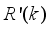
and
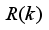
are the desired reference and the filtered reference signals respectively;
Am and
Bm are the denominator and numerator polynomials of the filter. In this way, the NAPC based on FNNO-MLMA is deigned, in part, based on the filter tracking error capability; where
Am and
Bm serves as tuning parameters used to improve the robustness and internal stability of the control algorithm respectively.
Assuming that at Assuming that the identified NNARMAX model is stable, proper and deterministic; then the NAPC based on FNNO-MLMA uses the linearized model parameters of the identified nonlinear NNARMAX model to accurately predict the current system output
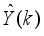
at that same sample time instant
k.
At time
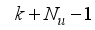
, the NAPC based on FNNO-MLMA calculates a sequence of control inputs
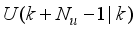
consisting of the current
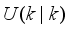
and future inputs
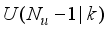
. The current input
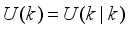
is held constant after
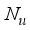
control moves; where
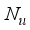
is the maximum control horizon. The input
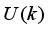
is calculated such that a set of
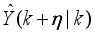
approaches the desired reference signal in an optimal manner over a specified prediction horizon
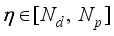
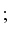
where
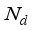
and
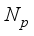
are the minimum and maximum prediction horizons respectively.
The predicted values are used to calculate the control signals by minimizing an objective function of the form:
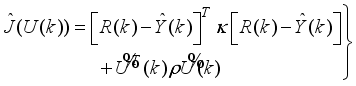 (65)
(65) subject to the constraints
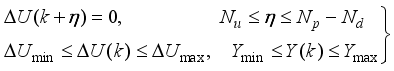 (66)
(66) where
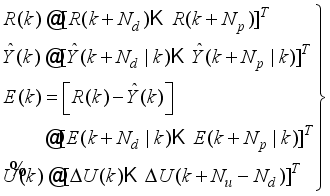 (67)
(67) where
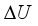
is the change in control signal;
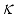
and
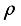
are two weighting matrices penalizing changes on
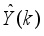
and
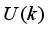
in Equation (
65).
4.1.2. The FNNO-MLMA for Nonlinear Adaptive Predictive Control
This section focuses on the development of the NAPC based on the FNNO-MLMA. Here we assume that
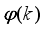
and NN model
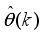
approximates the system (
37),
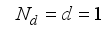
and that the system information is available up to time
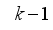
, so that the one step-ahead predictor of (
37) at time
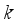
can be expressed as:
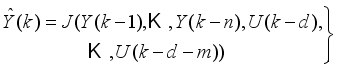 (68)
(68) So that the
η step-ahead model predictor from (
68) becomes:
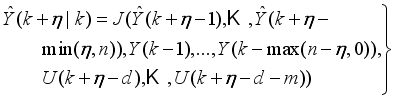 (69)
(69) The
η step-ahead predicted output of (
69) can be expressed in terms of nonlinear NN model parameters from (
44) as:
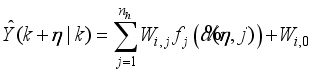 (70)
(70) where
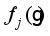
is given by (
11) but here
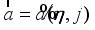
which is given as:
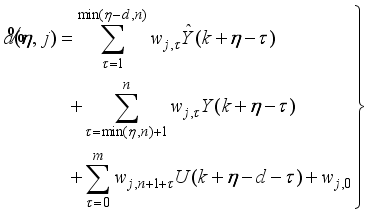 (71)
(71) 4.1.3. Computing the Past and Future Control Signals
The NAPC based on FNNO-MLMA proposed here computes the optimal future control signal based on nonlinear optimization using the nonlinear NNARMAX model developed in the previous section. The minimization of (
65) subject to the constraints defined by (
66) and (
67) can be expressed as:
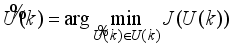 (72)
(72) The NN-based NAPC based on FNNO-MLMA proposed for solving (
72) is based on the FNNO method
| [35] | J. E. Dennis and R. B. Schnabel, “Numerical Methods for Unconstrained Optimization and Nonlinear Equations,” Englewood Cliffs, NJ: Prentice-Hall, 1996. |
| [37] | R. Fletcher, “Practical Methods of Optimization,” 2nd ed., Chichester: Wiley & Sons, 1987. |
[35, 37]
and the Levenberg-Marquardt method
| [41] | J. T. Spooner, M. Maggiore, R. Ordóñez and K. M. Passion, “Stable Adaptive Control and Estimation for Nonlinear Systems: Neural and Fuzzy Approximator Techniques,” New York: John Wiley & Sons, 2002. |
| [42] | O. M. Omidvar and D. L. Elliot, “Neural systems for control,” Academic Press, February, 1997. Available: http://www.isr.umd.edu/~delliot/NeuralSystemsForControl.pdf |
[41, 42]
with the following dynamic adaptive rule:
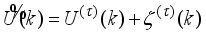 (73)
(73) which is applied for updating the sequence of future optimal control signal
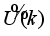
; where
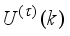
is the current iterate of the control sequence; and
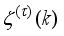
the search direction given by the following expression:
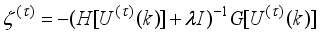 (74)
(74) where
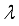
is the adaptation parameter,
I is a diagonal matrix;
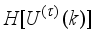
and
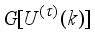
are the Hessian and Jacobian matrices given respectively by (
75) and (
76) as follows:
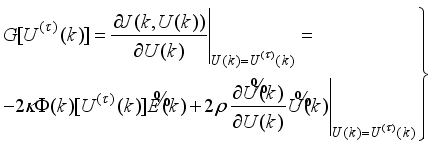 (75)
(75) 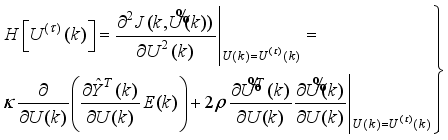 (76)
(76) where
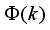
in (
75) is the partial derivatives of (
71).
To simplify the computation of
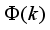
in (
75), the control signal is decomposed into the past and future control signals as
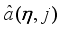
given in (
77) as follows:
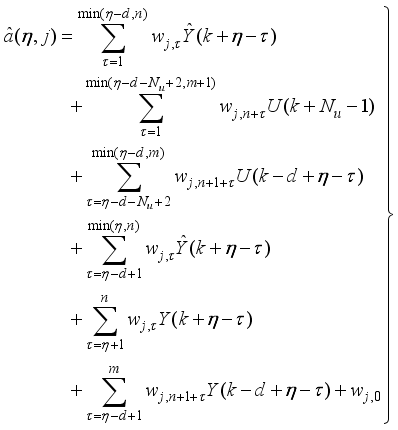 (77)
(77) The first three sums of (
77) depend on future control signals while the last three sums depend on past control signals.
Since the past control signals does not contribute to the output predictions because new measurements will be available at the next sample time
. Thus,
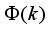
is computed here based only on the future control signals
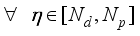
and
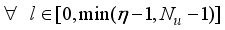
as:
where
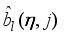
given in (
78) is computed from the first three sum of
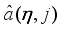
in (
77).
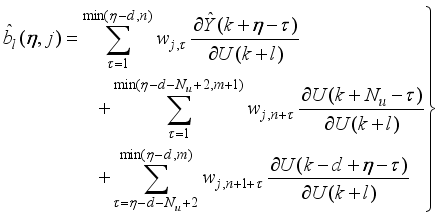 (78)
(78) The second-order derivative for all
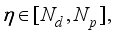
for all
, and for all
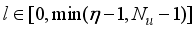
is calculated as follows:
where
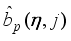
given in (
79) is again computed from the first three sum of
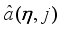
in (
77)
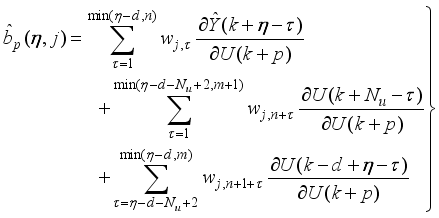 (79)
(79) where
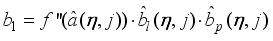
,
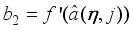
,
and
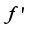
and
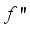
are the first and second derivatives of (
45).
4.1.4. Computing the Optimal Control Signal
The well-known problem with the Newton method is that the Hessian is not guaranteed to be positive definite in the open neighborhood of a global minimum. Thus, it is necessary to check that the Hessian is positive definite before updating the optimization. This implies checking for the definiteness of the Hessian matrix using:
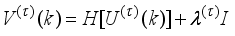 (80)
(80) Table 2.
Iterative Algorithm for Selecting  for Guaranteed Positive Definiteness of the Full Gauss-Newton Hessian Matrix.
for Guaranteed Positive Definiteness of the Full Gauss-Newton Hessian Matrix. Initialize:         , ,  , , , ,  to to  in step of in step of  . Compute (80) . Compute (80) for  to to  while  or or  , do , do for  to to  , do , do for  to to  , do , do 
if  , break, end if La,a , break, end if La,a for  to to  , do , do 
end for b, end for a if  , ,  , Re-compute (80) , Re-compute (80) for  to to  , do , do 
end for a else for  to to  , do , do 
for  to to  , do , do 
end for b, end for a, end for a, end if La,a, end for kn 
if  and and  , break, end , break, end end while  , end for , end for  |
to obtain a value of
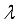
that will satisfy this condition. Again, many algorithms have been proposed for this purpose
| [23] | G. Colin, Y. Chamaillard, G. Bloch and G. Corde, “Neural control of fast nonlinear systems - Application to turbocharged SI engine with VCT,” IEEE Trans. Neu. Net., vol. 18, no. 4, pp. 1101 - 1114, Jul. 2007. |
| [28] | R. Chiong, “Intelligent Systems for Automated Learning and Application: Emerging Trends and Application,” Hershey PA, USA: Information Science Reference, 2010, ch. 4, pp. 204 - 316. |
| [29] | J. Wu, “Multilayer pottsperceptrons with Levenberg-Marquardt learning,” IEEE Trans. Neu. Net., vol. 19, no. 12, pp. 2032-2043, Dec. 2008. |
| [36] | M. T. Hagan and M. B. Menhaj, “Training feedforward network with the Marquardt algorithm,” IEEE Trans. Neu. Net., vol. 5, no. 6, pp. 989-993, Nov. 1994. |
[23, 28, 29, 36]
.
This paper proposes the adaptive algorithm given in
Table 2 which is based on the Cholesky factorization method which ensures that (
80) is always positive definite and none ill-conditioned. The algorithm first compute (
80) and check for positive definiteness. If this condition is not satisfied, the algorithm iteratively selects new
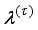
and re-computes (
80) and then terminates immediately positive definite of (
80) is achieved.
Having satisfied the positive definiteness of (
80), it is necessary to determine the optimal control signal as a global minimum. Again, the widely used method is the trust region approach mentioned earlier
| [37] | R. Fletcher, “Practical Methods of Optimization,” 2nd ed., Chichester: Wiley & Sons, 1987. |
[37]
. Here, we formulate the nonlinear minimization problem around the trust region as follows:
 (81)
(81) subject to
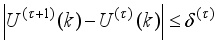 (82)
(82) where
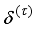
is the trust region radius where
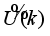
can be trusted.
The last issue to be addressed is related to how
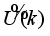
in (
81) is to be updated and the step size at the next iteration. Although, many algorithms have been proposed for this purpose
| [35] | J. E. Dennis and R. B. Schnabel, “Numerical Methods for Unconstrained Optimization and Nonlinear Equations,” Englewood Cliffs, NJ: Prentice-Hall, 1996. |
| [36] | M. T. Hagan and M. B. Menhaj, “Training feedforward network with the Marquardt algorithm,” IEEE Trans. Neu. Net., vol. 5, no. 6, pp. 989-993, Nov. 1994. |
| [37] | R. Fletcher, “Practical Methods of Optimization,” 2nd ed., Chichester: Wiley & Sons, 1987. |
[35-37]
, but here we reuse the
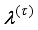
obtained from
Table 2 for this purpose. Note that
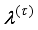
characterizes a hybrid adaptation parameter and has several effects as discussed in Section 3.1.3. Unlike in Section 3.1.3 where the approximated
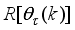
is guaranteed to be positive definite, here
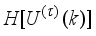
is not guaranteed to be non-positive definite or ill-conditioned and the algorithm of
Table 2 is used.
Thus, we reuse the
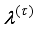
obtained in
Table 2 and apply the indirect method discussed in Section 3.1.4 to
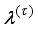
is adjusted according to the ratio
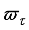
between the actual reduction
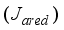
and theoretical predicted decrease
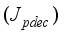
as defined below:
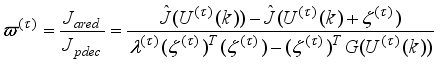 (83)
(83) Thus, we summarize the NAPC algorithm based on FNNO-MLMA in the following stepwise procedures:
1) Specify initial sequence of future control inputs
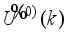
and evaluate
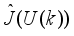
using (
65) subject to (
66). Initialize
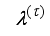
,
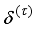
and set
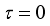
. while
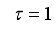
.
2) Compute
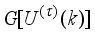
in (
75) and
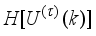
in (
76).
3) Compute the Cholesky factorization of the
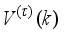
in (
80) using the algorithm of
Table 2.
4) Determine the search direction
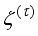
using (
77).
5) Evaluate
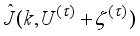
and compute
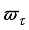
using (
83).
6) Update
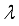
according to the conditions on
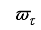
:
If
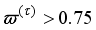
, then
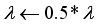
and go to
Step 7).
If
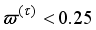
, then
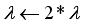
and go to
Step 7).
8) If
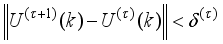
in (
82)
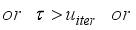
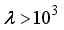
, go to
Step 9), else go to
Step 2).
9) Accept the sequence
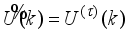
in (
81) subject to the constraints in (
66) and terminate the algorithm.
4.2. Discrete-Time Fixed-Parameter PID Controller Design for the NXT Robot Control
4.2.1. The PID Control Strategy
The constant gain or fixed-parameter proportional-integral-derivative (PID) controllers are widely used in many industries because of their simple structure, robust performance and the ease of their implementation
| [43] | A. Visioli, “Practical PID Control,” London: Springer-Verlag Ltd., 2006. |
| [44] | L. Wang, S. Chai, D. Yoo, L. Gan and K. Ng, “PID and Predictive Control of Electrical Drives and Power Converters using MATLAB®/SIMULINK®,” IEEE John Wiley & Sons Singapore Pte. Ltd, 2015. |
[43, 44]
.
In the simplest case, the NXT robot affected by the environmental disturbances can be controlled by a discrete-time fixed parameter PID controller used in a closed-loop configuration illustrated in
Figure 12. This operation is imitated by placing the NXT robot in the PID control loop.
Figure 12. The discrete-time fixed-parameter PID control scheme.
The mathematical relationship governing the discrete-time fixed-parameter PID controller that computes the control signal
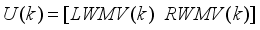
is defined as follows:
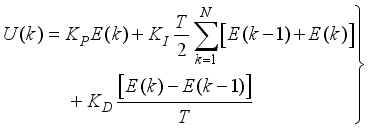 (84)
(84) where
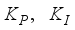
and
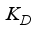
are the proportional, integral and derivative gains respectively,
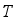
is the sampling time and
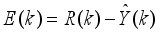
is the error term defined as the difference between the process
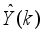
, filtered desired reference
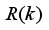
and N is the number of simulation samples (see sub-section 4.1.1).
The first, second and third terms in (
84) corresponds to the present, past and future control sequence respectively. The minimum and maximum constraints imposed on the PID controller to penalize changes on the NXT robot control inputs U (k) and NXT robot outputsY (k) are defined in (
66).
A major problem with PID controller is the “
wind up” of the integrator resulting in saturation of the integral term for control signal of large magnitude. Rich literatures exist for anti wind-up techniques to overcome this problem
| [43] | A. Visioli, “Practical PID Control,” London: Springer-Verlag Ltd., 2006. |
| [44] | L. Wang, S. Chai, D. Yoo, L. Gan and K. Ng, “PID and Predictive Control of Electrical Drives and Power Converters using MATLAB®/SIMULINK®,” IEEE John Wiley & Sons Singapore Pte. Ltd, 2015. |
[43, 44]
. According to this technique, the integrator switches off when the actuator output exceeds a predefined limit (i.e. saturated) subject to the constraints defined in (
66) and the update of the integral term is terminated.
4.2.2. The PID Control Law for the Servo Control of the NXT Robot
The starting point for the PID controller design for the NXT robot begins with the servo controller design. The servo controller is used as the preliminary controller for the NXTway-GS robot and where
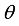
is selected as the reference signal for servo control. It is important to note that we cannot use variables other than
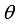
as the reference because the system may become uncontrollable. The block diagram of the preliminary servo controller for NXTway-GS robot is shown in
Figure 13.
We can now calculate the feedback (Kf) and integral (Ki) gains by the linear quadratic regulator (LQR) method. To achieve this, we choose the following weight matrix Q and R by experimental trial and error.
 (85)
(85) where Q (2, 2) is a weight for body pitch angle, and Q (5, 5) is a weight for time integration of difference between measured average angle and referenced one.
Furthermore, the value of the speed gain after LQR calculation needs to be adjusted because it fluctuates excessively when the NXT robot is in motion. In addition to the gain adjustment, the following control handles are added, namely:
1). Rotate NXTway-GS by giving different value to the left and right motor, and
2). Use Proportional (
P) control for wheel synchronization when NXT runs straightforward because the rotation angle of DC motors is not same even though same PWM is applied. Consequently, the NXT robot controller is derived as shown in the block diagram of
Figure 14. Here
,
and
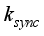
are the tuning parameters.
Figure 13. The Simulink® model of the NXT robot servo controller.
Servo control is a control technique such that that an output of a system tracks an expected behavior of the desired reference trajectory. PID control and I-PD control in classical control theory are a kind of servo control. It is necessary to add an integrator in the closed loop since it is necessary to track the desired output reference. The block diagram of servo control based on the PID scheme is shown in
Figure 13. The gains (controller parameters) of the servo controller can be calculated in the same way as feedback control by considering an expansion system. It has new state that is the difference between the output and referenced value. The servo control gains are derived as the following. The state equation and output function are given as the following:
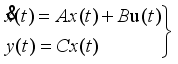 (86)
(86) We use a difference
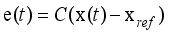
, an integral of the difference
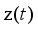
, states of the expansion system
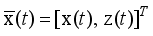
, and the orders of x and u are
n and
m respectively. The state equation of the expansion system is the following:
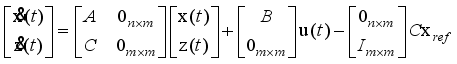 (87)
(87) If the expansion system is assumed to be stable, Equation (
39) converges to the following expression:
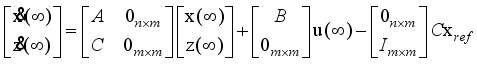 (88)
(88) By subtracting (
40) from (
39), the following state equation is obtained
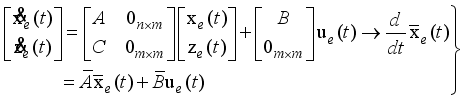 (89)
(89) where
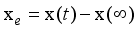
,
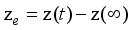
and
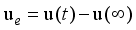
. We can use feedback control to make the expansion system stable. Thus, the control input is becomes
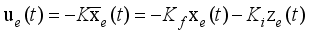 (90)
(90) If it is possible that
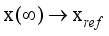
,
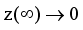
and
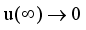
are assumed, the following input
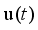
can be derived as:
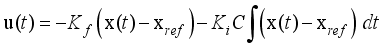 (91)
(91) Several literature on modern control engineering usually describe I-PD type expression (
in the first term of (
91) equals to zero) as servo control input
| [4] | K. Ogata, “Modern Control Engineering,” Pearson Education, Inc., Prentice Hall, Upper Saddle River, New Jersey, USA, 2010. |
| [5] | W. S. Levine, “The Control Handbook: Control System Advanced Methods,” Second Edition, CRC Press - Taylor & Francis Group, New York, USA, 2011. |
| [6] | N. S. Nise, “Control Systems Engineering,” Seventh Edition, John Wiley & Sons Inc., California, USA. |
[4-6]
. However, we use discrete-time fixed-parameter PID type expression as (
91) to improve the reference tracking performance.
5. NNARMAX Model Identification Using OWA-MLMA Based on AGNA and Adaptive Control Using NAPC Based on FNNO-MLMA of the NXT Robot
5.1. Performance Comparison of the NNARMAX Model Identification of the NXT Robot Model Using OWA-MLMA and INCBPA, Results and Discussions
5.1.1. NNARMAX Model Identification of the NXT Robot Using OWA-MLMA and INCBPA
In this study, the inputs to the NXT robot are the left wheel motor voltage (
LWMV) and right wheel motor voltage (
RWMV), that is
U = [
LWMVRWMV]
T. The outputs of the NXT robot are the left wheel rotation angle (
LWRA) and the right wheel rotation angle (
RWRA), that is
. The input vector
to the NNARMAX model predictor consists of the regression vectors
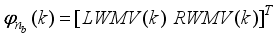
,
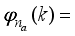
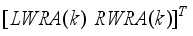
and
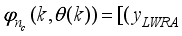
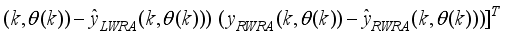
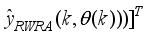
. The outputs of the NNARMAX model predictor are the predicted values of
LWRA and
RWRA given as
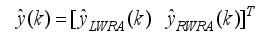
.
As discussed in Section 2.2.3, an open loop simulation of the NXT robot MATLAB/Simulink model is performed to obtain 250,000 input-output data pair. The data is split into
N = 1750,000 training and 75,000 validation data. The training data is scaled to zero mean and unit variance to prevent signals of largest magnitudes from dominating the identified model [wastewater papers
| [30] | V. A. Akpan and R. A. O. Osakwe, “Multivariable NNARMAX Model Identification of an AS-WWTP Using ARLS (Part 1: Dynamic Modeling of the Biological Reactors),” American J. of Int. Sys., vol. 4, no. 2, pp. 43 - 72, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140402.03.pdf |
| [31] | V. A. Akpan and R. A. O. Osakwe, “Multivariable NNARMAX Model Identification of an AS-WWTP Using ARLS (Part 2: Dynamic Modeling of the Secondary Settler and Clarifier),” American J. of Int. Sys., vol. 4, no. 3, pp. 77 - 106, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140403.02.pdf |
| [32] | V. A. Akpan and R. A. O. Osakwe, “Online Prediction of Influent Characteristics for Wastewater Treatment Plants Management Using Adaptive Recursive NNARMAX Model,” American J. of Int. Sys., vol. 4, no. 3, pp. 107 - 130, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140403.03.pdf |
[30-32]
. Again, the joint weights are rescaled afterwards so that the trained network can work with unscaled test data.
For training and assessing the convergence performance of the network, the following parameters are selected:
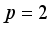
,
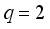
,
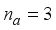
,
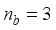
,
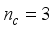
,
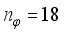
for the NNARMAX model predictors as well as
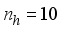
,
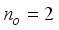
,
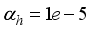
and
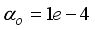
. The details of these parameters are discussed in section 3; where
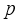
and
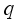
are the number of inputs and outputs of the system,
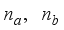
and
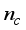
are the orders of the regressors,
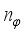
is the total number of regressors (that is, the total number of inputs to the network),
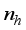
and
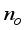
are the number of hidden and output layers neurons, and
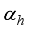
and
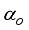
are the hidden and output layers weight decay terms. Also,
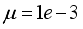
is selected to initialize the INCBPA while
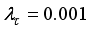
,
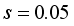
and
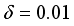
are arbitrarily selected to initialize the OWA-MLMA. The network is trained for
τ = 20 iterations with the just mentioned selected parameters.
5.1.2. Validation of the Trained Network: Results and Discussion
The convergences of the OWA-MLMA based on AGNA and the INCBPA from NNARMAX model training to capture the NXT robot model are shown in
Figure 15. It can be seen in
Figure 15, INCBPA shows faster but poor convergences with smaller computation times as shown in the second row of
Table 3 when compared to OWA-MLMA. The superior convergences of the OWA-MLMA compared to the INCBPA are shown in
Figure 15 with much smaller minimum performance index (MPI) at the expense of higher computation time.
Figure 15. Convergence and minimum performance index comparison of the OWA-MLMA based on AGNA and INCBPA training algorithms for 20 iterations for the NXT robot modeling.
Table 3. Performance comparison of the INCBPA and OWA-MLMA training results.
S/N | Performance Evaluation Parameters | Left wheel rotation angle | Right wheel rotation angle |
INCBPA | OWA-MLMA | INCBPA | OWA-MLMA |
1 | Computation time for model identification (sec) | 5.8120e+02 | 1.5109e+03 | 5.7036e+02 | 1.3225e+03 |
2 | Minimum performance index (MPI) | 5.2343e-02 | 4.4952e-05 | 2.6659e-02 | 8.0105e-05 |
3 | Total square error (TSE) | 4.1499e+01 | 9.5898e-03 | 1.1104e+01 | 2.6953e-03 |
4 | Mean error of one step ahead prediction of training data | 1.0442e-01 | 1.1104e-04 | 7.0847e-01 | 2.6953e-04 |
5 | Mean error of one step prediction of test data | 3.2832e+01 | 5.1594e-02 | 2.8006e+01 | 1.1955e-03 |
6 | Mean value of 5-step ahead prediction error | 4.8886e+01 | 5.0041e-02 | 5.1418e+01 | 5.0736e-02 |
7 | Akaike’s final prediction error (AFPE) estimate | 3.7989e+01 | 9.8119e-02 | 5.1532e+01 | 1.4494e-02 |
The total square error (TSE) discussed in Subsection 3.1.1, for the network trained with the INCBPA and the OWA-MLMA algorithms are given in the fourth row of
Table 3. The OWA-MLMA has a much smaller TSE when compared to the INCBPA algorithm. These much smaller values of the TSE and the MPIs indicate that OWA-MLMA performs better than the INCBPA for the same number of iterations. These much smaller errors suggest that the model identified by the OWA-MLMA approximates the NXT robot much better than the INCBPA model.
1) Validation by the One-Step Ahead Predictions Simulation using Scaled Training Data
In the one-step ahead prediction method, the errors obtained from one-step ahead output predictions of the trained network are assessed. In
Figure 16, the graphs for the one-step ahead predictions of the scaled training data (blue -) against the trained network output predictions (red --*) using the NNARMAX models trained by INCBPA and proposed OWA-MLMA.
The mean value of the one-step ahead prediction errors are given in the fifth row of
Table 3. It can be seen in the figures that the network predictions of the training data almost closely match the original training data. Although, the scaled training data prediction errors by both algorithms are small, the proposed OWA-MLMA appears to have a much smaller error when compared to the INCBPA as shown in the fifth row of
Table 3. These small one-step ahead prediction errors are indications that the networks trained using the OWA-MLMA captures and approximate the nonlinear dynamics of the NXT robot to a high degree of accuracy. This is further justified by the small mean values of the TSE obtained for the networks trained using the proposed OWA-MLMA for the NXT robot as shown in the fourth row of
Table 3.
2) Validation by the One-Step Ahead Predictions Simulation using Unscaled Test Data
Furthermore, the suitability of the INCBPA and the proposed OWA-MLMA for NNARMAX model identification for use with the NXT robot is investigated by validating the trained network with the 75,000 unscaled dynamic test data. Graphs of the trained network predictions (red --*) of the test data with the actual test data (blue -) using the INCBPA and the proposed OWA-MLMA are shown in
Figure 17(a) and (b) for the left and right wheels respectively. The test data predictions prove the effectiveness of these algorithms. The prediction accuracies of the unscaled test data by the networks trained using the INCBPA and the proposed OWA-MLMA evaluated by the computed mean prediction errors shown in the sixth row of
Table 3. Again, one can observe that the test data predictions errors obtained with the model trained by the proposed OWA-MLMA appears much smaller when compared to those obtained by the model trained using the INCBPA. The predictions of the unscaled test data given in
Figure 17 as well as the mean value of the one step ahead test data prediction errors in the six row of
Table 3 verifies the NN ability to model accurately the dynamics of the NXT robot using the proposed OWA-MLMA training algorithm.
Figure 16. Comparison of one-step ahead output predictions by the trained network (red --*) with the scaled original training data (blue -) for (a) left and (b) right wheel rotation angle angles by OWA-MLMA based on AGNA and INCBPA training algorithms.
3) K-Step Ahead Prediction Simulations using Unscaled Training Data
The third method of validation is the K-step ahead predictions where the outputs of the trained network are compared to the unscaled output training data
| [30] | V. A. Akpan and R. A. O. Osakwe, “Multivariable NNARMAX Model Identification of an AS-WWTP Using ARLS (Part 1: Dynamic Modeling of the Biological Reactors),” American J. of Int. Sys., vol. 4, no. 2, pp. 43 - 72, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140402.03.pdf |
| [31] | V. A. Akpan and R. A. O. Osakwe, “Multivariable NNARMAX Model Identification of an AS-WWTP Using ARLS (Part 2: Dynamic Modeling of the Secondary Settler and Clarifier),” American J. of Int. Sys., vol. 4, no. 3, pp. 77 - 106, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140403.02.pdf |
| [32] | V. A. Akpan and R. A. O. Osakwe, “Online Prediction of Influent Characteristics for Wastewater Treatment Plants Management Using Adaptive Recursive NNARMAX Model,” American J. of Int. Sys., vol. 4, no. 3, pp. 107 - 130, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140403.03.pdf |
[30-32]
. The results of the K-step ahead output predictions (red --*) using the K-step ahead prediction validation method for 5-step ahead output predictions (that is K = 5) compared with the unscaled training data (blue -) are shown in
Figure 18(a) and 18(b) for the networks trained using the INCBPA and the proposed OWA-MLMA. The value K = 5 is chosen since it is a typical value used in most model predictive control (MPC) applications
| [30] | V. A. Akpan and R. A. O. Osakwe, “Multivariable NNARMAX Model Identification of an AS-WWTP Using ARLS (Part 1: Dynamic Modeling of the Biological Reactors),” American J. of Int. Sys., vol. 4, no. 2, pp. 43 - 72, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140402.03.pdf |
| [31] | V. A. Akpan and R. A. O. Osakwe, “Multivariable NNARMAX Model Identification of an AS-WWTP Using ARLS (Part 2: Dynamic Modeling of the Secondary Settler and Clarifier),” American J. of Int. Sys., vol. 4, no. 3, pp. 77 - 106, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140403.02.pdf |
| [32] | V. A. Akpan and R. A. O. Osakwe, “Online Prediction of Influent Characteristics for Wastewater Treatment Plants Management Using Adaptive Recursive NNARMAX Model,” American J. of Int. Sys., vol. 4, no. 3, pp. 107 - 130, 2014. Available: http://article.sapub.org/pdf/10.5923.j.ajis.20140403.03.pdf |
[30-32]
. The comparison of the 5-step ahead output predictions performance by the network trained using the INCBPA and the proposed OWA-MLMA algorithms indicate the superiority of the proposed OWA-MLMA over the INCBPA.
Figure 17. Comparison of one-step ahead output predictions by the trained network (red --*) with the unscaled test data (blue -) for (a) left and (b) right wheel rotation angles by OWA-MLMA based on AGNA and INCBPA training algorithms.
The computations of the mean value of the K-step ahead prediction error (MVPE) are given in the seventh row of
Table 3 by the network trained using INCBP and the proposed OWA-MLMA respectively. The smaller MVPE of the 5-step ahead predictions are indications that the trained network approximates the dynamics of the NXT robot to a high degree of accuracy with the networks of both algorithms but with the network based on the OWA-MLMA giving much smaller distant prediction errors.
4) Akaike’s Final Prediction Error (AFPE) Estimates
The implementation of the AFPE algorithm for the regularized criterion
| [17] | V. A. Akpan, “Development of new model adaptive predictive control algorithms and their implementation on real-time embedded systems,” Aristotle university of Thessaloniki, GR-54124, Thessaloniki, Greece, Ph.D. Dissertation, 517 pages, July, 2011. Available: http://invenio.lib.auth.gr/record/127274/files/GRI-2011-7292.pdf |
| [27] | L. Lung, “System Identification: Theory for the User,” 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 1999. |
| [45] | J. Sjöberg and L. Ljung, “Overtraining, regularization, and searching for minimum in neural networks,” Int. J. of Cont., vol. 62: 1391-1408, 1995. |
[17, 27, 45]
for the network trained using the INCBP and the proposed OWA-MLMA with multiple weight decay gives their respective AFPE estimates which are listed in the eighth row of
Table 3. These relatively small values of the AFPE estimate indicate that the trained networks capture the underlying dynamics of the aerobic reactor of the NXT robot and that the network is not over-trained
| [27] | L. Lung, “System Identification: Theory for the User,” 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 1999. |
| [45] | J. Sjöberg and L. Ljung, “Overtraining, regularization, and searching for minimum in neural networks,” Int. J. of Cont., vol. 62: 1391-1408, 1995. |
[27, 45]
. This in turn implies that optimal network parameters have been selected including the weight decay parameters. Again, the results of the AFPE estimates computed for the networks trained using the proposed OWA-MLMA are much smaller when compared to those obtained using INCBPA.
Table 4. The NXT robot constraints for adaptive control.
Constraint Parameters | Fixed-Parameter PID Controller | NAPC based on FNNO-MLMA |
LWRA | RWRA | LWRA | RWRA |
Minimum control input (umin) | -10 | -10 | -10 | -10 |
Maximum control input (umax) | 10 | 10 | 10 | 10 |
Minimum predicted output (ymin) | -0.5 | -0.5 | -0.5 | -0.5 |
Maximum predicted output (ymax) | 10 | 10 | 10 | 10 |
Minimum desired reference (Refmin) | -100 | -100 | -100 | -100 |
Maximum desired reference (Refmax) | 100 | 100 | 100 | 100 |
Table 5. The NXT robot controller tuning parameters.
Tuning Parameters | Fixed-Parameter PID Controller | NAPC based on FNNO-MLMA |
LWRA | RWRA | LWRA | RWRA |
ICI (u) | -80 | -80 | -10 | -10 |
IPO (y) | 0 | 0 | 0 | 0 |
Nd | - | 1 | 1 | 1 |
Nu | - | 2 | 3 | 2 |
Np | - | 5 | 7 | 5 |
Κ | - | 1 | 1.5 | 1 |
ρ | - | 0.8 | 0.08 | 0.08 |
λ | - | - | 0.1 | 0.7 |
Am | [1-0.7] | [1-0.7] | [1-0.7] | [1-0.7] |
Bm | [00.3] | [00.3] | [00.3] | [00.3] |
Globmin | - | - | 7 | 5 |
δ | - | - | 1e-6 | 1e-4 |
uiter | - | - | 10 | 8 |
KP | 30 | - | - | - |
KI | 500 | - | - | - |
KD | 100 | - | - | - |
*ICI = Initial control input; IPO = Initial predicted output.
Figure 18. Comparison of 5-step ahead output predictions by the trained network (red --*) with the unscaled original training data (blue -) for (a) left and (b) right wheel rotation angle by OWA-MLMA based on AGNA and INCBPA training algorithms.
5.2. Performance Comparison of the Off-Line Closed-Loop Model Identification and Control of the NXT Robot Using NAPC and PID: Results and Discussion
The main control objective here is to ensure that the NXT robot movement closely follows the prescribed designed reference trajectory without overshoot, oscillation or prolonged time lag.
Initially, the NNARMAX model of the NXT robot is identified and validated as in the previous subsection to obtain the optimal network parameters. The fixed-parameter PID and the NAPC based on FNNO-MLMA controllers are then simulated off-line separately for 400 simulation samples subject to the constraints in
Table 4 using the NNARMAX model of the NXT robot to obtain the optimal tuning parameters given in
Table 5. The data used for the off-line model identification and control is the experimental data obtained from the open-loop MATLAB/Simulink simulation.
The off-line closed-loop PID and the NAPC control performances of the
LWRA and
RWRA output predictions are shown in
Figure 19(a) and (b) respectively while the control inputs
LWMV and
RWMV settings are shown in
Figure 19(c) and (d) respectively. The output prediction errors due to the PID and NAPC controllers are shown in
Figure 19(e) and (f) respectively for quick comparison. In these simulations, we allow the constraints on the maximum predicted outputs to be +100° for both
LWRA and
RWRA as shown in
Table 5 in order to observe any overshoot. As it can be seen in
Figure 19(a) and (b), the NAPC based on FNNO-MLMA shows good control performance over the fixed-parameter PID. The fixed-parameter PID exhibits a very large overshoots of 310° for both
LWRA and
RWRA trajectory tracking with all-round oscillations and hardly track the desired reference signals as evident in
Figure 19(a) and (b) as well as significant output prediction errors which is shown in
Figure 19(e) and (f). The very large overshoot exhibited by the fixed-parameter PID of
Figure 19(a) and (b) results in a serious penalty on the control signals with sudden sharp spike on the voltage source as shown in
Figure 19(c) and (d). In
Figure 19(a) and (b), one can also observe the extremely difficulty and poor ability of the fixed-parameter PID to track the desired reference trajectory at the 11
th and 5
th sampling time instant for
LWRA and
RWRA respectively. The poor performance of the fixed-parameter PID controller is due to the highly nonlinear behaviour of the NXT robot couple with the abrupt and sudden change of the NXT robot navigations as defined by the desired reference trajectory.
5.3. Online Closed-Loop Identification and Control of the NXT Robot Using NAPC Based on FNNO-MLMA, Results and Discussion
The online closed-loop NAPC based on the FNNO-MLMA control performance for the
LWRA and
RWRA output predictions for 280 simulation samples are shown in
Figure 20(a) and (b) while the control inputs,
LWMV and
RWMV are shown in
Figure 20(c) and (d). As it can be seen in
Figure 20, the NAPC based on FNNO-MLMA shows good control performance with accurate tracking of the prescribed desired reference trajectory without any overshoots or oscillations. The minimum control efforts of the NAPC based on FNNO-MLMA is evident in
Figure 20(c) and (d). It can be agreed that the excellent performance of the online closed-loop implementation of the proposed OWA-MLMA neural network training algorithm combined with the NAPC based on the FNNO-MLMA indicates their suitability for online nonlinear model identification and adoptive control for the NXT robot and can be adapted for other nonlinear applications.
Figure 19. Off-line NXT robot output predictions by PID (blue -) and nonlinear APC (black.-) for (a) LWRA and (b) RWRA with the manipulated signals (c) LWMV and (d) RWMV to track the desired reference signal (red -). Output prediction errors by PID (blue -) and NAPC (black.-) for (e) LWRA) and (f) RWRA.
The combined OWA-MLMA based on AGNA for NNARMAX model identification and NAPC based on FNNO-MLMA for adaptive control were implemented on an Intel® Core™2 CPU running at 1.86 GHz under two conditions. The first condition is their direct serial implementation using MATLAB and the obtained computation times are shown in
Figure 21(a). The minimum and maximum computation times are 17.8351 and 45.2167 seconds with an average computation time of 31.5259 seconds.
The second condition is their parallel implementation using the MATLAB “
parpool” command available in the MATLAB Distributed and Parallel Toolbox
. The obtained computation times are shown in
Figure 21(b). The minimum and maximum computation times are 3.5962 and 5.2273 seconds with an average computation time of 4.4117 seconds.
The “parpool” command implements the loop specified by the command in parallel and it uses the four Intel® processors available on the computer system. This MATLAB facility from the Distributed and Parallel Computing Toolbox allows the utilization of the four processors available on the computer for the implementation of the identification and control algorithm at each sampling time step.
Figure 20. Output predictions for the Online closed-loop implementation of the OWA-MLMA model identification and nonlinear APC based on FNNO-MLMA controller for the NXT robot: reference trajectory (blue o) and NAPC (red.) for (a) LWRA and (b) RWRA with the manipulated signals (c) LWMV and (d) RWMV.
As it can be observed in
Figure 21, the parallel implementation of the online closed-loop identification and NAPC control reduces the computation time for NXT robot model identification and adaptive control by 7.1460 times when compared to the serial implementation. The reduced computation time is still higher than the sampling time of the NXT robot of 0.5 seconds and this may limit the use of NXT robots for in real-time applications with strict time constraints in an industrial environment. The online closed-loop identification and NAPC control algorithms could be implemented on a field programmable gate array (FPGA) which would significantly reduce the computation times such that model identification and adaptive control algorithm can be repeated severally within a single sampling time instant before updating the NXT robot for stable adaptive control under different disturbances
| [47] | V. A. Akpan, D. Chasapis and G. D. Hassapis, “FPGA Implementation of Neural Network-Based AGPC for Nonlinear F-16 Aircraft Auto-Pilot Control: Part 1 - Modeling, Synthesis, Verification and FPGA-in-the-Loop Co-Sim,” American J. of Emb. Sys. & Appl., vol. 9, no. 1, pp. 6-36 pages, 2022. Available: https://www.sciencepg.com/journal/paperinfo?journalid=236&doi=10.11648/j.ajesa.20220901.13 |
| [48] | V. A. Akpan, D. Chasapis and G. D. Hassapis, “FPGA Implementation of Neural Network-Based AGPC for Nonlinear F-16 Aircraft Auto-Pilot Control: Part 2 - Implementation of Embedded PowerPC™440 with AGPC,” American J. of Emb. Sys. & Appl., vol. 9, no. 2, pp. 37-65, 2022. Available: https://www.sciencepublishinggroup.com/journal/paperinfo?journalid=236&doi=10.11648/j.ajesa.20220902.11 |
[47, 48]
.
Figure 21. Computation time for the implementation of the OWA-MLMA training algorithm and the nonlinear APC based on FNNO-MLMA control algorithm: (a) series and (b) parallel implementation.
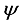 is the body pitch angle,
is the body pitch angle, 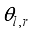 is the wheel angle (where l and r indicates left and right angles), and
is the wheel angle (where l and r indicates left and right angles), and 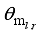 is the DC motor angle. The physical parameters of the NXT robot are defined in Table 1.
is the DC motor angle. The physical parameters of the NXT robot are defined in Table 1. 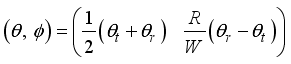 (1)
(1) 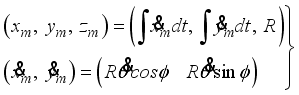 (2)
(2) 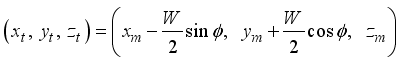 (3)
(3) 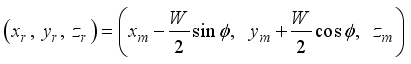 (4)
(4) 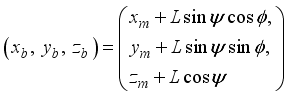 (5)
(5) 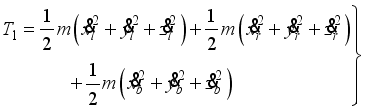 (6)
(6) 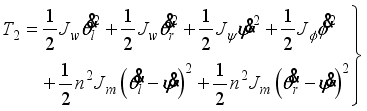 (7)
(7) 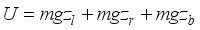 (8)
(8) 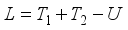 (9)
(9) 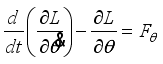 (10)
(10) 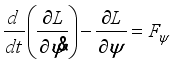 (11)
(11) 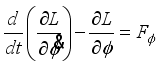 (12)
(12) 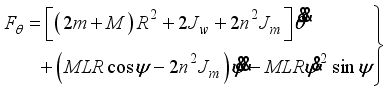 (13)
(13) 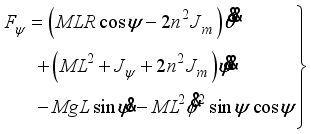 (14)
(14) 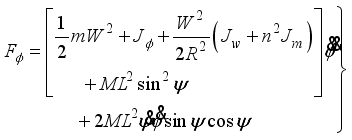 (15)
(15) 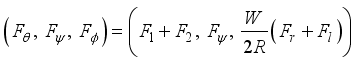 (16)
(16) 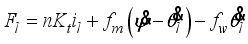 (17)
(17) 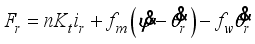 (18)
(18)  (19)
(19) 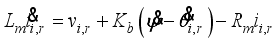 (20)
(20) 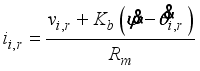 (21)
(21) 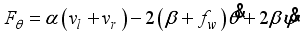 (22)
(22) 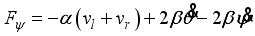 (23)
(23) 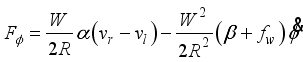 (24)
(24) 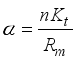 and
and 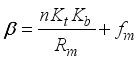 (25)
(25) 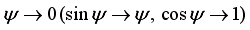 and neglect the second-order term like
and neglect the second-order term like 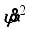 . The motion equations (13-15) are approximated according to the following equations respectively:
. The motion equations (13-15) are approximated according to the following equations respectively: 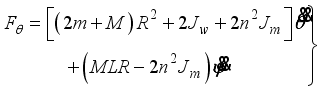 (26)
(26) 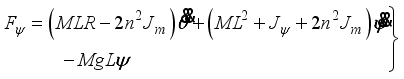 (27)
(27)  (28)
(28) 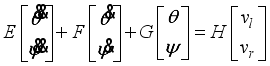 (29)
(29) 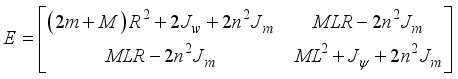
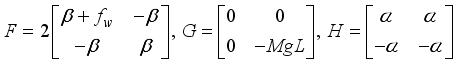
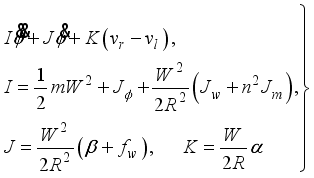 (30)
(30) 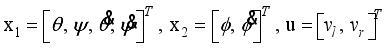 (31)
(31) 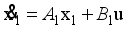 (32)
(32) 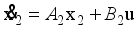 (33)
(33)  (34)
(34) 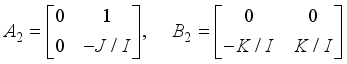 (35)
(35) 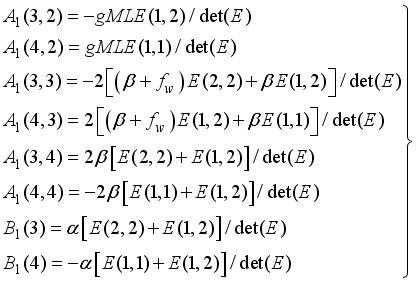 (36)
(36) 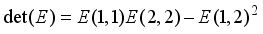
 and the body pitch angular velocity
and the body pitch angular velocity  . It is easy to evaluate
. It is easy to evaluate 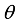 and
and 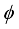 by using
by using 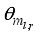 . There are two methods to evaluate
. There are two methods to evaluate 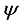 by using
by using 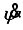 , namely: 1). Derive
, namely: 1). Derive 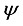 by integrating the angular speed numerically and 2). Estimate
by integrating the angular speed numerically and 2). Estimate 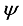 by using an observer based on modern control theory. In this study, we use the second method in the following for the controller design chiefly because of easy stability establishment.
by using an observer based on modern control theory. In this study, we use the second method in the following for the controller design chiefly because of easy stability establishment. 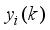 of a discrete-time nonlinear m-input n-output multivariable system at time instant k responding to the lth input
of a discrete-time nonlinear m-input n-output multivariable system at time instant k responding to the lth input 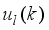 can be described by the following Nonlinear AutoRegressive Moving Average with eXogeneous input (NARMAX) model:
can be described by the following Nonlinear AutoRegressive Moving Average with eXogeneous input (NARMAX) model: 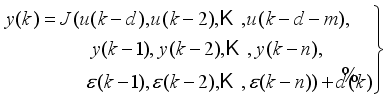 (37)
(37)  is a nonlinear function of its input arguments assumed to be differentiable,
is a nonlinear function of its input arguments assumed to be differentiable, 
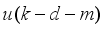 ,
, 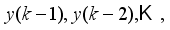
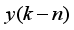 and
and 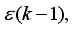
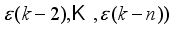 are the vectors of the past input, past output and past prediction error values respectively while
are the vectors of the past input, past output and past prediction error values respectively while  are the disturbances and d is the system delay. Assuming that the input-output data pair
are the disturbances and d is the system delay. Assuming that the input-output data pair 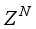 of the system taken over NT period of time is available
of the system taken over NT period of time is available  (38)
(38) 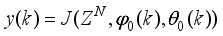 (39)
(39) 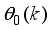 is a known vector of appropriate dimension that defines the parameters of the system and
is a known vector of appropriate dimension that defines the parameters of the system and 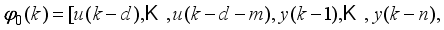
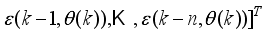 is the state (regression) vector at time
is the state (regression) vector at time 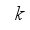 .
. 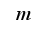 ,
, 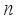 , with an initial small random value of
, with an initial small random value of 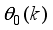 ; at time
; at time 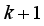 we can construct a predictor
we can construct a predictor 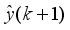 that will produce the a priori predictor estimate of (39)
that will produce the a priori predictor estimate of (39) 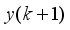 based on the state of the system
based on the state of the system 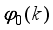 at time
at time 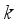 can be define as
can be define as 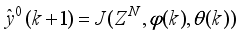
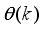 is an unknown adjustable parameter vector of appropriate dimension and the regression (state) vector
is an unknown adjustable parameter vector of appropriate dimension and the regression (state) vector 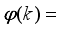
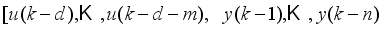
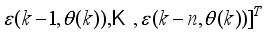 . Thus, at time
. Thus, at time 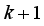 a new value of
a new value of 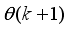 will be known and the a posteriori predictor estimate can be computed as
will be known and the a posteriori predictor estimate can be computed as 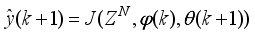 (40)
(40) 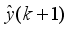 is compared to the system output
is compared to the system output 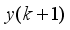 and the error
and the error 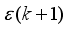 between the two outputs is minimized and used to adjust and update
between the two outputs is minimized and used to adjust and update 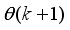 such that
such that 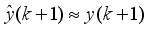 . It is evident that the predictor output depends on
. It is evident that the predictor output depends on  . For notational convenience, we define the error here as:
. For notational convenience, we define the error here as: 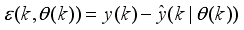 (41)
(41) 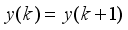 ,
, 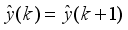 and
and 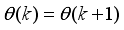 are the true system output, network predicted output and the adjustable parameters of the network. Thus, the determination and adjustment of
are the true system output, network predicted output and the adjustable parameters of the network. Thus, the determination and adjustment of 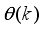 becomes an unconstrained nonlinear minimization problem defined here as:
becomes an unconstrained nonlinear minimization problem defined here as: 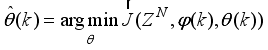 (42)
(42) 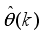 is the value of
is the value of 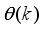 that minimizes (42) and
that minimizes (42) and 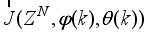 is formulated as a total square error (TSE) type cost function given as:
is formulated as a total square error (TSE) type cost function given as: 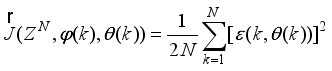 (43)
(43) 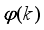 which is obtained from
which is obtained from 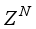 defined in (38).
defined in (38). 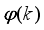 in (42) is decomposed into the past input, past output and past prediction error parts
in (42) is decomposed into the past input, past output and past prediction error parts 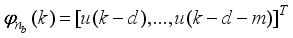 ,
, 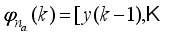
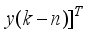 and
and 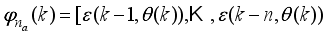 respectively. The outputs of the NN model of Figure 10 can be expressed in terms of the network parameters as:
respectively. The outputs of the NN model of Figure 10 can be expressed in terms of the network parameters as: 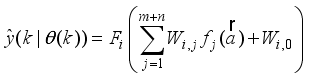 (44)
(44) 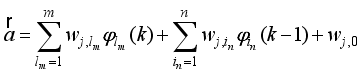
 and
and  and
and 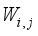 are the hidden and output weights respectively;
are the hidden and output weights respectively; 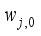 and
and 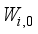 are the hidden and output biases;
are the hidden and output biases; 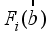 is a linear activation function for the output layer and
is a linear activation function for the output layer and 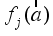 is an hyperbolic tangent activation function for the hidden layer given here as:
is an hyperbolic tangent activation function for the hidden layer given here as: 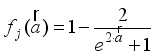 (45)
(45)  .
. 
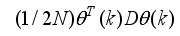 ; where
; where 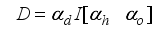 ,
, 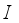 is an identity matrix,
is an identity matrix, 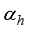 and
and 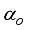 are the weight decay values for the input-to-hidden and hidden-to-output layers respectively. Using (44), the regularized criterion from (43) becomes:
are the weight decay values for the input-to-hidden and hidden-to-output layers respectively. Using (44), the regularized criterion from (43) becomes: 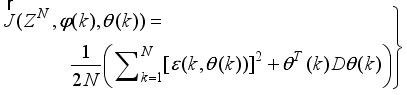 (46)
(46) 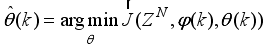 (47)
(47)  can be presented to the training algorithm at each time step. The most popular way being the batch (off-line) mode where all the data set
can be presented to the training algorithm at each time step. The most popular way being the batch (off-line) mode where all the data set 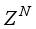 is evaluated at each time step and the recursive (online) mode where each data pair of
is evaluated at each time step and the recursive (online) mode where each data pair of 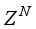 is evaluated at each time step.
is evaluated at each time step. 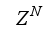 at each sampling time step and all the data are evaluated in batch mode at each sampling time step.
at each sampling time step and all the data are evaluated in batch mode at each sampling time step. 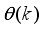 and updates
and updates  iteratively according to the following typical updating rule:
iteratively according to the following typical updating rule: 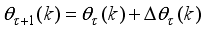 (48)
(48)  denotes
denotes  at the current iteration
at the current iteration 
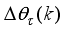 is the searching direction,
is the searching direction, 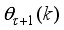 is the global minimum and
is the global minimum and 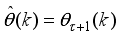 if certain stopping criteria are satisfied.
if certain stopping criteria are satisfied. 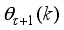 is the back-propagation algorithm (BPA)
is the back-propagation algorithm (BPA) 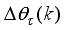 directly proportional to the negative of the gradient of (46) evaluated at
directly proportional to the negative of the gradient of (46) evaluated at 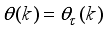 . Using (46) and (48), the basic BP algorithm can be stated as:
. Using (46) and (48), the basic BP algorithm can be stated as: 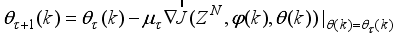 (49)
(49) 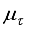 is the step size and
is the step size and  is the gradient NN training using the BPA has been reported to be characterized by poor performance
is the gradient NN training using the BPA has been reported to be characterized by poor performance 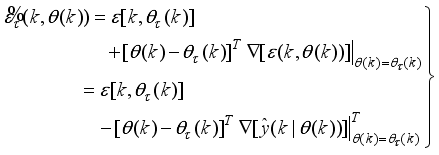 (50)
(50) 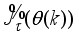 given as
given as 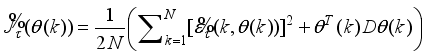 (51)
(51) 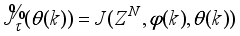 from now on shall be used for convenience. Note that Equation (17) can also be expressed as
from now on shall be used for convenience. Note that Equation (17) can also be expressed as 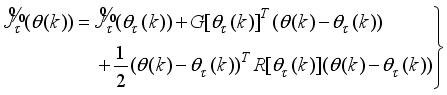 (52)
(52) 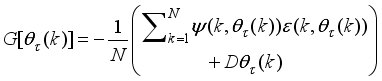 (53)
(53) 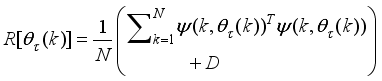 (54)
(54)  and
and 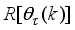 are the gradient and exact Gauss-Newton Hessian matrices respectively, and
are the gradient and exact Gauss-Newton Hessian matrices respectively, and 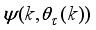
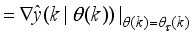 denotes the derivative of the network output with respect to
denotes the derivative of the network output with respect to 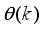 evaluated at
evaluated at 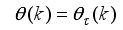 . By substituting
. By substituting 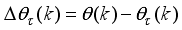 into (52) and setting its derivative to zero as follows:
into (52) and setting its derivative to zero as follows: 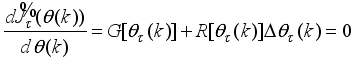
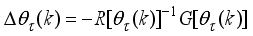 (55)
(55) 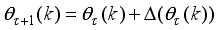 (56)
(56) 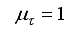 . Equation (54) is guaranteed to be positive definite since it is based a second-order approximation of (47) which is well-known to be positive definite
. Equation (54) is guaranteed to be positive definite since it is based a second-order approximation of (47) which is well-known to be positive definite 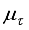 especially when
especially when 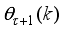 is far from
is far from 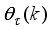 and (53) can sometimes be ill-conditioned. In the next sub-section, we utilize (56) to formulate the proposed OWA-MLMA based on AGNA which addresses the above issues dynamically.
and (53) can sometimes be ill-conditioned. In the next sub-section, we utilize (56) to formulate the proposed OWA-MLMA based on AGNA which addresses the above issues dynamically. 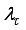 to the diagonal of
to the diagonal of 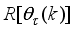 with a new updating rule given as
with a new updating rule given as 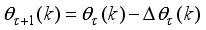 (57)
(57) 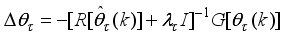 (58)
(58)  characterizes a hybrid of searching directions and has several effects
characterizes a hybrid of searching directions and has several effects  , Equation (57) reduces to the steepest descent algorithm (with step
, Equation (57) reduces to the steepest descent algorithm (with step  which requires a descend search method; and 2). for small values of
which requires a descend search method; and 2). for small values of 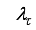 , Equation (57) reduces to Gauss-Newton algorithm (with step given by (56)).
, Equation (57) reduces to Gauss-Newton algorithm (with step given by (56)). 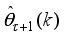 is large
is large 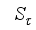 , so that (58) becomes
, so that (58) becomes 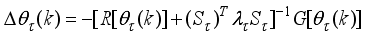 (59)
(59) 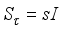 is adjusted simultaneously with
is adjusted simultaneously with 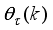 in the search for
in the search for 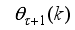 by (57), s is the scaling parameter, and I is an identity. The solution to (57) using (59) based on the trust region method
by (57), s is the scaling parameter, and I is an identity. The solution to (57) using (59) based on the trust region method 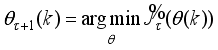 (60)
(60) 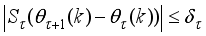 .
. 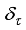 is the trust region radius within which
is the trust region radius within which 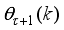 can be found. A difficulty with the Levenberg-Marquardt method is in selecting and adjusting the parameter
can be found. A difficulty with the Levenberg-Marquardt method is in selecting and adjusting the parameter 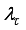 as well as how
as well as how 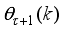 should be updated. The choice for the proper selection of
should be updated. The choice for the proper selection of 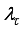 has led to the formulation of several algorithms
has led to the formulation of several algorithms 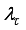 is adjusted based on the ratio
is adjusted based on the ratio 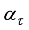 between the actual reduction
between the actual reduction 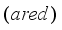 and theoretical predicted decrease
and theoretical predicted decrease 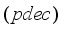 subject to the constraint in (60) stated here as:
subject to the constraint in (60) stated here as: 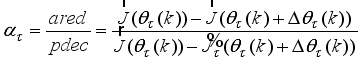 (61)
(61) 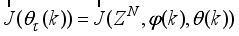 in (46) for convenience.
in (46) for convenience. 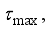 D,
D, 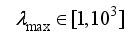 and m and n for
and m and n for 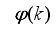 .
. 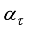 in (61).
in (61). 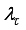 according to the following conditions on
according to the following conditions on 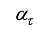 :
: 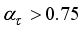 , then
, then 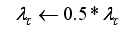 and go to Step6).
and go to Step6). 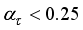 , then
, then 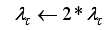 and go to Step 6).
and go to Step 6). 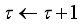 and
and 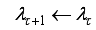 .
. 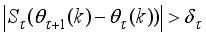 or
or 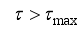 or
or 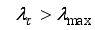 (number of iterations); go to Step 8), else go to Step 3).
(number of iterations); go to Step 8), else go to Step 3). 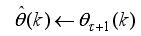 and terminate.
and terminate. 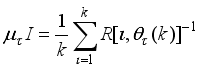 (62)
(62) 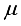 is the step size and
is the step size and  is an identity matrix of appropriate dimension. Next, the basic back-propagation given as
is an identity matrix of appropriate dimension. Next, the basic back-propagation given as 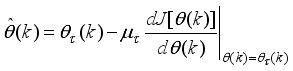 (63)
(63) 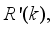
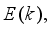
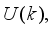
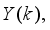
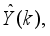
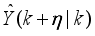 ,
, 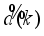 and
and 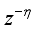 are the desired reference signal, prediction error, control input, system output, η step-delay prediction model output, η step-ahead predicted output, noise/input disturbances and ηstep-delay operator respectively and k is the number of samples based on the new measurement data sample.
are the desired reference signal, prediction error, control input, system output, η step-delay prediction model output, η step-ahead predicted output, noise/input disturbances and ηstep-delay operator respectively and k is the number of samples based on the new measurement data sample. 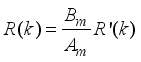 (64)
(64) 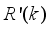 and
and 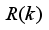 are the desired reference and the filtered reference signals respectively; Am and Bm are the denominator and numerator polynomials of the filter. In this way, the NAPC based on FNNO-MLMA is deigned, in part, based on the filter tracking error capability; where Am and Bm serves as tuning parameters used to improve the robustness and internal stability of the control algorithm respectively.
are the desired reference and the filtered reference signals respectively; Am and Bm are the denominator and numerator polynomials of the filter. In this way, the NAPC based on FNNO-MLMA is deigned, in part, based on the filter tracking error capability; where Am and Bm serves as tuning parameters used to improve the robustness and internal stability of the control algorithm respectively. 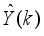 at that same sample time instant k.
at that same sample time instant k. 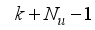 , the NAPC based on FNNO-MLMA calculates a sequence of control inputs
, the NAPC based on FNNO-MLMA calculates a sequence of control inputs 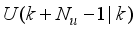 consisting of the current
consisting of the current 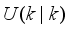 and future inputs
and future inputs 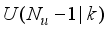 . The current input
. The current input 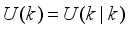 is held constant after
is held constant after 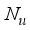 control moves; where
control moves; where 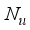 is the maximum control horizon. The input
is the maximum control horizon. The input 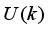 is calculated such that a set of
is calculated such that a set of 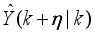 approaches the desired reference signal in an optimal manner over a specified prediction horizon
approaches the desired reference signal in an optimal manner over a specified prediction horizon 
 where
where  and
and 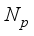 are the minimum and maximum prediction horizons respectively.
are the minimum and maximum prediction horizons respectively. 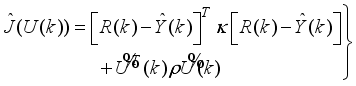 (65)
(65) 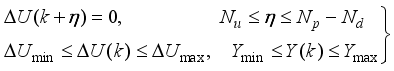 (66)
(66) 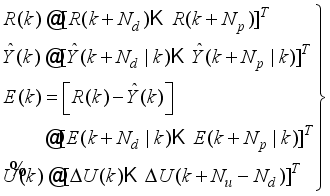 (67)
(67) 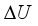 is the change in control signal;
is the change in control signal; 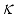 and
and 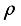 are two weighting matrices penalizing changes on
are two weighting matrices penalizing changes on 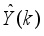 and
and 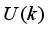 in Equation (65).
in Equation (65). 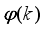 and NN model
and NN model 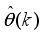 approximates the system (37),
approximates the system (37), 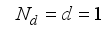 and that the system information is available up to time
and that the system information is available up to time 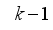 , so that the one step-ahead predictor of (37) at time
, so that the one step-ahead predictor of (37) at time 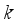 can be expressed as:
can be expressed as: 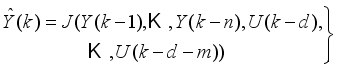 (68)
(68) 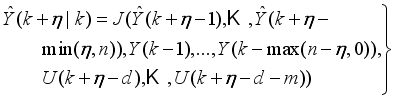 (69)
(69) 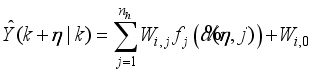 (70)
(70) 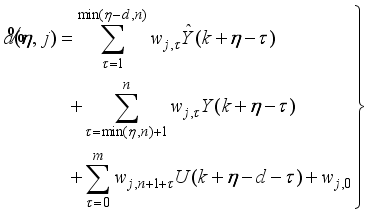 (71)
(71) 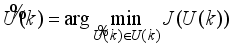 (72)
(72) 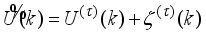 (73)
(73) 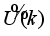 ; where
; where 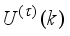 is the current iterate of the control sequence; and
is the current iterate of the control sequence; and 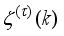 the search direction given by the following expression:
the search direction given by the following expression: 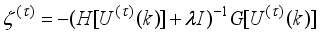 (74)
(74) 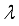 is the adaptation parameter, I is a diagonal matrix;
is the adaptation parameter, I is a diagonal matrix; 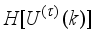 and
and 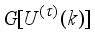 are the Hessian and Jacobian matrices given respectively by (75) and (76) as follows:
are the Hessian and Jacobian matrices given respectively by (75) and (76) as follows: 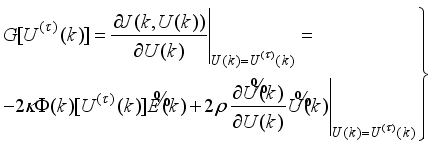 (75)
(75) 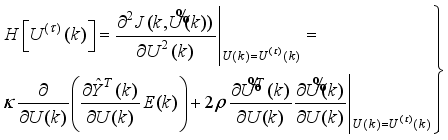 (76)
(76) 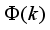 in (75), the control signal is decomposed into the past and future control signals as
in (75), the control signal is decomposed into the past and future control signals as  given in (77) as follows:
given in (77) as follows: 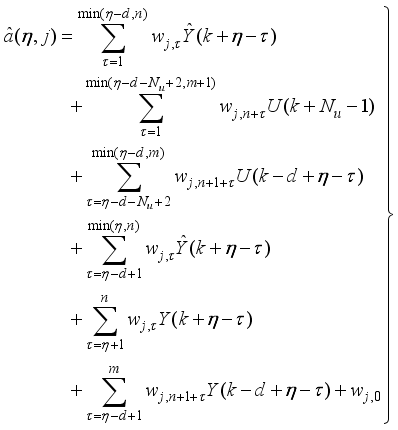 (77)
(77) 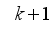 . Thus,
. Thus, 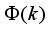 is computed here based only on the future control signals
is computed here based only on the future control signals 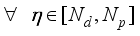 and
and 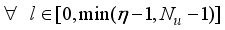 as:
as: 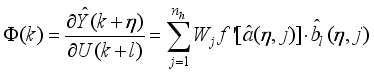
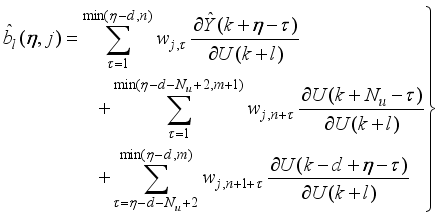 (78)
(78)  for all
for all  , and for all
, and for all 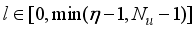 is calculated as follows:
is calculated as follows: 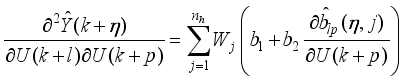
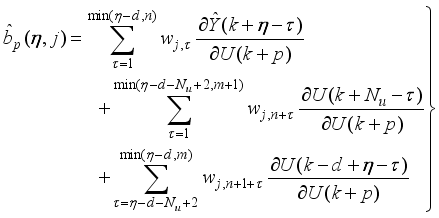 (79)
(79) 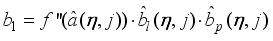 ,
, 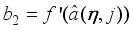 ,
, 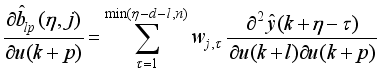
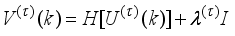 (80)
(80)  that will satisfy this condition. Again, many algorithms have been proposed for this purpose
that will satisfy this condition. Again, many algorithms have been proposed for this purpose 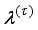 and re-computes (80) and then terminates immediately positive definite of (80) is achieved.
and re-computes (80) and then terminates immediately positive definite of (80) is achieved.  (81)
(81) 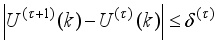 (82)
(82) 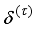 is the trust region radius where
is the trust region radius where 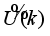 can be trusted.
can be trusted. 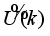 in (81) is to be updated and the step size at the next iteration. Although, many algorithms have been proposed for this purpose
in (81) is to be updated and the step size at the next iteration. Although, many algorithms have been proposed for this purpose 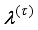 obtained from Table 2 for this purpose. Note that
obtained from Table 2 for this purpose. Note that 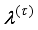 characterizes a hybrid adaptation parameter and has several effects as discussed in Section 3.1.3. Unlike in Section 3.1.3 where the approximated
characterizes a hybrid adaptation parameter and has several effects as discussed in Section 3.1.3. Unlike in Section 3.1.3 where the approximated 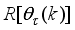 is guaranteed to be positive definite, here
is guaranteed to be positive definite, here 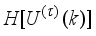 is not guaranteed to be non-positive definite or ill-conditioned and the algorithm of Table 2 is used.
is not guaranteed to be non-positive definite or ill-conditioned and the algorithm of Table 2 is used. 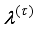 obtained in Table 2 and apply the indirect method discussed in Section 3.1.4 to
obtained in Table 2 and apply the indirect method discussed in Section 3.1.4 to 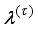 is adjusted according to the ratio
is adjusted according to the ratio 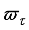 between the actual reduction
between the actual reduction 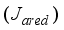 and theoretical predicted decrease
and theoretical predicted decrease 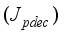 as defined below:
as defined below: 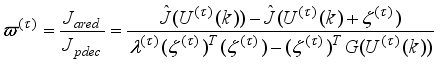 (83)
(83) 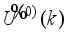 and evaluate
and evaluate 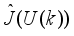 using (65) subject to (66). Initialize
using (65) subject to (66). Initialize 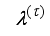 ,
, 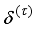 and set
and set 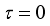 . while
. while 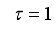 .
. 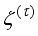 using (77).
using (77). 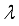 according to the conditions on
according to the conditions on 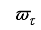 :
: 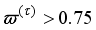 , then
, then 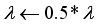 and go to Step 7).
and go to Step 7). 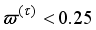 , then
, then 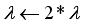 and go to Step 7).
and go to Step 7). 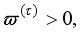 update
update 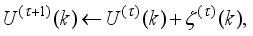 and set
and set  .
. 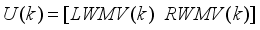 is defined as follows:
is defined as follows: 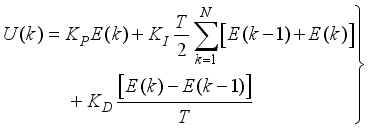 (84)
(84) 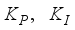 and
and 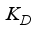 are the proportional, integral and derivative gains respectively,
are the proportional, integral and derivative gains respectively, 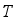 is the sampling time and
is the sampling time and 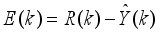 is the error term defined as the difference between the process
is the error term defined as the difference between the process 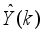 , filtered desired reference
, filtered desired reference 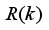 and N is the number of simulation samples (see sub-section 4.1.1).
and N is the number of simulation samples (see sub-section 4.1.1). 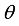 is selected as the reference signal for servo control. It is important to note that we cannot use variables other than
is selected as the reference signal for servo control. It is important to note that we cannot use variables other than 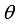 as the reference because the system may become uncontrollable. The block diagram of the preliminary servo controller for NXTway-GS robot is shown in Figure 13.
as the reference because the system may become uncontrollable. The block diagram of the preliminary servo controller for NXTway-GS robot is shown in Figure 13. 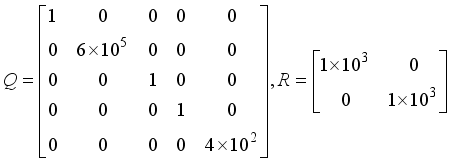 (85)
(85) 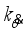 ,
, 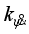 and
and 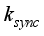 are the tuning parameters.
are the tuning parameters. 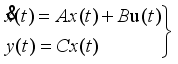 (86)
(86) 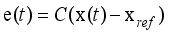 , an integral of the difference
, an integral of the difference 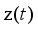 , states of the expansion system
, states of the expansion system 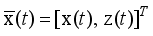 , and the orders of x and u are n and m respectively. The state equation of the expansion system is the following:
, and the orders of x and u are n and m respectively. The state equation of the expansion system is the following: 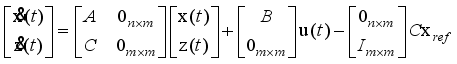 (87)
(87) 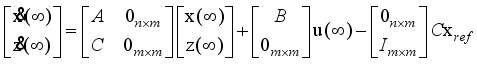 (88)
(88) 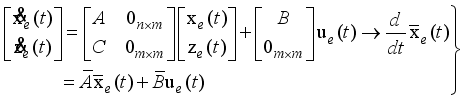 (89)
(89) 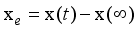 ,
, 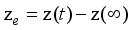 and
and 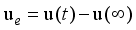 . We can use feedback control to make the expansion system stable. Thus, the control input is becomes
. We can use feedback control to make the expansion system stable. Thus, the control input is becomes 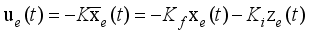 (90)
(90) 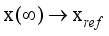 ,
, 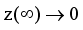 and
and 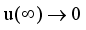 are assumed, the following input
are assumed, the following input 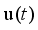 can be derived as:
can be derived as: 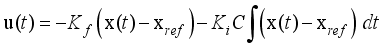 (91)
(91) 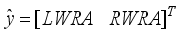 . The input vector
. The input vector  to the NNARMAX model predictor consists of the regression vectors
to the NNARMAX model predictor consists of the regression vectors 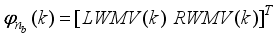 ,
, 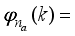
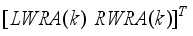 and
and 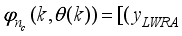
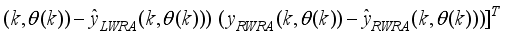
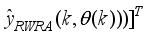 . The outputs of the NNARMAX model predictor are the predicted values of LWRA and RWRA given as
. The outputs of the NNARMAX model predictor are the predicted values of LWRA and RWRA given as 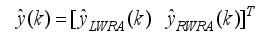 .
.  ,
,  ,
, 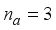 ,
, 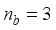 ,
, 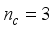 ,
, 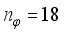 for the NNARMAX model predictors as well as
for the NNARMAX model predictors as well as 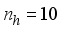 ,
, 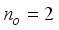 ,
, 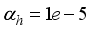 and
and 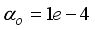 . The details of these parameters are discussed in section 3; where
. The details of these parameters are discussed in section 3; where 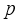 and
and 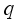 are the number of inputs and outputs of the system,
are the number of inputs and outputs of the system, 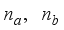 and
and 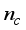 are the orders of the regressors,
are the orders of the regressors, 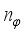 is the total number of regressors (that is, the total number of inputs to the network),
is the total number of regressors (that is, the total number of inputs to the network), 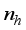 and
and 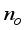 are the number of hidden and output layers neurons, and
are the number of hidden and output layers neurons, and 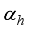 and
and 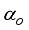 are the hidden and output layers weight decay terms. Also,
are the hidden and output layers weight decay terms. Also, 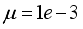 is selected to initialize the INCBPA while
is selected to initialize the INCBPA while 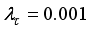 ,
, 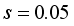 and
and 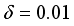 are arbitrarily selected to initialize the OWA-MLMA. The network is trained for τ = 20 iterations with the just mentioned selected parameters.
are arbitrarily selected to initialize the OWA-MLMA. The network is trained for τ = 20 iterations with the just mentioned selected parameters.