Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology

Augustine Oghenekevwe Igbinake

doi:doi:10.11648/j.ae.20250901.13

Research Article |

| Peer-Reviewed

Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology

Augustine Oghenekevwe Igbinake^*

Published in Applied Engineering (Volume 9, Issue 1)

Received: 12 April 2025 Accepted: 27 April 2025 Published: 4 June 2025

Views: Downloads:

Download PDF

Share This Article

Twitter
Linked In
Facebook

Abstract

Specific heat, an intrinsic thermal property, represents the amount of heat energy required to raise the temperature of a substance by one degree Celsius. Accurate estimation of specific heat in welded metals is crucial for understanding thermal behavior during and after welding processes, especially in applications where temperature control and energy efficiency are essential. This study focuses on the prediction and optimization of the specific heat of mild steel weldments using Response Surface Methodology (RSM), a statistical technique for modeling and analyzing the effects of multiple variables. A total of 100 welded mild steel specimens, each measuring 60 mm × 40 mm × 10 mm, were prepared through controlled Tungsten Inert Gas (TIG) welding operations. During the experiments, key process parameters - welding current, arc voltage, and shielding gas flow rate - were systematically varied to observe their effect on specific heat. The experimental data collected were analyzed using Design Expert 13 software, enabling statistical modeling, regression analysis, and optimization. A second-order quadratic model was developed to describe the relationship between specific heat and the input parameters. The optimal parameter combination was determined to be 180 A, 19 V, and 13 L/min, resulting in a predicted specific heat value of 445.106 J/kg°C. The developed model provides a useful predictive tool for future thermal analysis of welded structures.

Published in	Applied Engineering (Volume 9, Issue 1)
DOI	10.11648/j.ae.20250901.13
Page(s)	37-44
Creative Commons	This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited.
Copyright	Copyright © The Author(s), 2025. Published by Science Publishing Group

Keywords

Weldment, Specific Heat, Mild Steel, Temperature, Current, Gas Flow Rate

1. Introduction

Specific heat characterizes the thermal response of a material by indicating the amount of heat required to raise its temperature by one degree Celsius. This fundamental property plays a crucial role in thermal and energy-related processes and is vital for understanding how materials behave under thermal conditions. It is especially significant for engineers and scientists working in fields such as welding, heat treatment, casting, and thermal energy storage

[1]

. In metals, including steel, specific heat influences thermal conductivity, expansion, and the development of thermal gradients during processes like welding.

Theoretical models for estimating specific heat have evolved over time, incorporating both classical and quantum mechanical principles. Einstein’s model, which assumes uniform vibrational frequencies for all atoms, effectively predicts heat capacity at moderate to high temperatures (T > 102 K). However, its accuracy diminishes at lower temperatures due to the rapid decay of specific heat with temperature

[2]

. To address this, Debye’s model introduces a distribution of vibrational modes (phonons), capturing the T³ dependence of specific heat at cryogenic temperatures, thus improving the accuracy at low temperatures

[2]

. These models provide a foundational understanding of specific heat behavior, though in engineering applications, they are often simplified for practical use.

Experimental determination of specific heat is typically performed through calorimetry or differential scanning techniques, measuring enthalpy changes with respect to temperature. However, in metals, these measurements are complicated by additional effects such as lattice vibrations, electronic excitations, and magnetic contributions, especially at low temperatures

[3, 4]

. Parkinson

[3]

and Jones

[4]

highlighted that in alloys such as α-brasses, electron-lattice interactions contribute linear terms to the heat capacity, complicating its evaluation. These physical complexities underscore the need for accurate, systematic methods for the experimental and analytical determination of specific heat, particularly in multi-phase and welded structures.

In welding, specific heat becomes even more critical. Understanding heat transfer dynamics is essential for predicting melting behavior, cooling rates, and residual stress development in welded joints. Tungsten Inert Gas (TIG) welding, known for its precision, requires careful management of thermal input to prevent defects. As reported by Zhao et al.

[5]

, the specific heat of the base material significantly impacts thermal distortion during welding. In addition, welding parameters such as current, voltage, and shielding gas flow have direct effects on melting efficiency and the heat-affected zone (HAZ) characteristics

[6, 7]

. Studies have shown that optimizing these parameters can improve weld pool geometry and reduce thermal defects, thus enhancing weld quality and performance

[8]

Response Surface Methodology (RSM), a statistical optimization tool, has proven effective in modeling multi-variable welding processes. RSM helps develop predictive models that identify optimal conditions for welding, leading to improved thermal and mechanical properties. This method has been widely applied to optimize welding parameters such as melting efficiency, weld bead geometry, and thermal input

[7, 8]

This study aims to address the gap in understanding by using RSM to develop a predictive model for estimating the specific heat of mild steel (S275) weldments under controlled TIG welding conditions. By systematically varying key process parameters and analyzing their interactions, this research seeks to improve control over thermal properties, thereby contributing to enhanced weld integrity, reduced thermal distortion, and improved energy efficiency in welding processes.

2. Materials and Methods

Central Composite Design (CCD) matrix was used to gather data from the sets of experiments; the specimen was produced from mild steel plates and welded with the TIG process.

2.1. Materials

The set of tools, including power hacksaw cutting and grinding machines, a mechanical vice, emery (sand) paper, and a sander presented in Figure 1 was used to prepare the mild steel coupons for welding.

Download: Download full-size image

Figure 1. Set of equipment for coupon preparation.

The tungsten inert gas welding equipment presented in Figure 2 was used to weld the plates after the edges had been machined and bevelled.

Download: Download full-size image

Figure 2. Tungsten Inert Gas Welding Equipment.

2.2. Methods

According to experimental matrix presented in Table 2, twenty sets of experiment were performed using 5 specimens for each run. The plate samples were 40mm x 60 mm long with a thickness of 10mm. The samples were cut longitudinally with a single-V joint preparation as shown in Figure 3

[9]

Download: Download full-size image

Figure 3. Weld specimen design.

2.2.1. Design of Experiment

The key input parameters considered in this work were welding current, voltage, and gas flow rate. In contrast, the response or measured parameters include impact energy, weld undercut, ambient temperature, solidus temperature, liquidus temperature, tensile strain, thermal conductivity, specific heat, weld density and thermal diffusivity. The range and level

[10, 11]

of the experimental variables were obtained and are presented in Table 1.

Table 1. Range and Levels of independent variables.

Independent Variables	Range and Levels of Input Variables
Independent Variables	Lower Range (-1)	Upper Range (+1)
Welding Current (Amp) X₁	150	180
Welding Voltage (Volt) X₂	16	19
Gas flow rate (lit/min) X₃	13	16

Using the range and levels of the independent variables presented in Table 1, the statistical design of the experiment (DoE) using the central composite design (CCD) method was done. Experimental design was done with the aid of design expert version 13. The total number of experimental runs that can be generated using the CCD is calculated by the formula

[12]

N= 2^k+n_c+ 2k(1)

where,

N = the number of experimental runs based on CCD design

2^k = the number of factorial points

n_c = the number of center points

2k = the number of axial points

k = the number of input variables

Using Equation 1, twenty (20) experimental runs were generated and presented in Table 2.

Table 2. Design of experiment (DoE) Matrix.

Std	Run	Current (A)	Voltage (V)	Gas flow rate (lit/min)
15	1	165.000	17.500	14.500
16	2	180.000	16.000	16.000
17	3	150.000	19.000	16.000
18	4	165.000	17.500	14.500
19	5	165.000	17.500	14.500
20	6	165.000	20.023	14.500
9	7	180.000	19.000	16.000
10	8	165.000	17.500	14.500
11	9	150.000	19.000	13.000
12	10	165.000	17.500	14.500
13	11	180.000	16.000	13.000
14	12	139.773	17.500	14.500
1	13	180.000	19.000	13.000
2	14	165.000	14.977	14.500
3	15	190.227	17.500	14.500
4	16	165.000	17.500	11.977
5	17	165.000	17.500	17.023
6	18	150.000	16.000	13.000
7	19	150.000	16.000	16.000
8	20	165.000	17.500	14.500

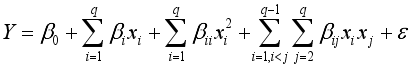2.2.2. Data Collection

Welding was done after grinding and polishing the sample edges, and the responses were measured and recorded. The input variable measured corresponding to the measured response is presented in Table 3. The TIG welding process, thermal measurements, post-weld tests and calculations were conducted,

2.2.3. Data Analysis

The Response surface methodology (RSM) expert models were employed to analyse the data. For design data analysis, Design Expert Statistical Software, Version 13.0, was employed to obtain the effects, coefficients, standard deviations of coefficients, and other statistical parameters of the fitted models. The behaviour of the system, which was used to evaluate the relationship between the response variables (Ys) and the independent variables (X1, X2, and X3), was explained using the empirical second-order polynomial equation

[13]

(2)

where,

X₁, X₂, X₃… X_k = input variables;

Y, β₀, β_i, β_ii, and β_ij = the known parameters, and ƹ = the random error.

The Response Surface Methodology (RSM) is a variation of simple linear regression, with the incorporation of the second-order effects of non-linear relationships. It is a popular optimization technique for determining the best possible combinations of variables to determine a specific response to a phenomenon. RSM is particularly useful for understanding the relationship between multiple predictor variables and multiple predicted responses.

3. Result and Discussion

The experimental results utilized in the Response Surface Methodology are presented in Table 3.

Table 3. Measured response corresponding to input variables.

S/N	I, Amp	E, Volt	GFR (Lmin)	Specific heat J/(Kg°C)
1	165.000	17.500	14.500	323.763
2	180.000	16.000	16.000	357.843
3	150.000	19.000	16.000	408.963
4	165.000	17.500	14.500	306.723
5	165.000	17.500	14.500	323.763
6	165.000	20.023	14.500	426.004
7	180.000	19.000	16.000	477.124
8	165.000	17.500	14.500	306.723
9	150.000	19.000	13.000	289.682
10	165.000	17.500	14.500	323.763
11	180.000	16.000	13.000	340.803
12	139.773	17.500	14.500	261.816
13	180.000	19.000	13.000	451.407
14	165.000	14.977	14.500	312.937
15	190.227	17.500	14.500	393.636
16	165.000	17.500	11.977	350.167
17	165.000	17.500	17.023	424.566
18	150.000	16.000	13.000	269.086
19	150.000	16.000	16.000	338.884
20	165.000	17.500	14.500	318.343

To validate the suitability of the quadratic model for analyzing the experimental data, the sequential model sum of squares was calculated for the specific heat capacity response, as presented in Table 4. The Quadratic vs. 2FI source was selected as the highest-order polynomial source where the additional terms are significant and the model is not aliased.

Table 4. Sequential model sum of square for specific heat capacity.

Source	Sum of Squares	Df	Mean Square	F-value	p-value
Mean vs Total	2.454E+06	1	2.454E+06
Linear vs Mean	49959.41	3	16653.14	13.58	0.0001
2FI vs Linear	5521.47	3	1840.49	1.70	0.2166
Quadratic vs 2FI	13221.68	3	4407.23	50.37	< 0.0001	Suggested
Cubic vs Quadratic	504.76	4	126.19	2.04	0.2069	Aliased
Residual	370.24	6	61.71
Total	2.524E+06	20	1.262E+05

To test how well the quadratic model can explain the underlying variation associated with the experimental data, the lack of fit test was estimated for each response. A model with a significant lack of fit cannot be employed for prediction. The computed lack of fit for the specific heat is presented in Table 5. The selected model should have a p-value higher than 0.05, showing insignificant lack of fit.

Table 5. Lack of fit test for Specific heat capacity.

Source	Sum of Squares	Df	Mean Square	F-value	p-value
Linear	19268.09	11	1751.64	25.02	0.0012
2FI	13746.62	8	1718.33	24.54	0.0013
Quadratic	524.93	5	104.99	1.50	0.3337	Suggested
Cubic	20.17	1	20.17	0.2882	0.6144	Aliased
Pure Error	350.07	5	70.01

Table 6 presents the model statistics computed for the Specific Heat response based on the model sources. The suggested model exhibits an R² of 0.9874, an Adjusted R² of 0.9761, and a Predicted R² of 0.9308, indicating a strong model fit and high predictive capability.

Table 6. Model summary statistics for Specific heat capacity.

Source	Std. Dev.	R²	Adjusted R²	Predicted R²	PRESS
Linear	35.02	0.7180	0.6652	0.5520	31171.42
2FI	32.93	0.7974	0.7039	0.4845	35866.98
Quadratic	9.35	0.9874	0.9761	0.9308	4817.94	Suggested
Cubic	7.86	0.9947	0.9831	0.9288	4950.88	Aliased

A one-way analysis of variance (ANOVA) table was generated to assess the strength of the quadratic mode lin minimizing the specific heat. The Model F-value of 87.24 implies the model is significant. There is only a 0.01% chance that an F-value this large could occur due to noise. P-values less than 0.0500 indicate model terms are essential. A, B, C, AB, AC, B², and C² are significant model terms. In this case, Values greater than 0.1000 indicate the model terms are not significant. If there are many insignificant model terms (not counting those required to support hierarchy), model reduction may improve the model. The Lack of Fit F-value of 1.50 implies the Lack of Fit is insignificant relative to the pure error. There is a 33.37% chance that a Lack of Fit F-value this large could occur due to noise. A non-significant lack of t is good

[14]

. The computed standard error measures the difference between the experimental and corresponding predicted terms. Coefficient statistics for specific heat response variables and the coefficient estimate represent the expected change in response per unit change in factor value when all remaining factors are held constant. The intercept in an orthogonal design is the overall average response of all the runs. The coefficients are adjustments around that average based on the factor settings. When the factors are orthogonal; the VIFs are 1; VIFs greater than 1 indicate multi-colinearity, and the higher the VIF, the more severe the correlation of factors. As a rough rule, VIFs less than 10 are tolerable.

A variance inflation factor (VIF) value of 1.00 for the individual and combined terms and 1.02 for the quadratic terms, as observed, indicates a significant model in which the variables are highly correlated with the responses. The optimal equation, which shows the individual effects and combines interactions of the selected input variables Variance inflation factor (VIF) value of 1.00 for the individual and combined terms, 1.02 for the quadratic terms as observed, indicate a significant model in which the variables are highly correlated with the responses.

The optimal equation, which shows the individual effects and combines interactions of the selected input variables (current, voltage and gas flow rate) against the measured specific heat, is presented based on the coded variables in Equation 3.

Y_{s} = + 317.10 + 39.71 A + 37.40 B + 26.14 C + 17.40 AB - 18.29 AC + 7.27 BC + 4.26 A^{2} + 19.02 B^{2} + 25.35 C^{2}

(3)

Where, Ys = Specific heat

To diagnose the statistical properties of the response surface model, the normal probability plot of residual for specific heat is presented in Figure 4.

Download: Download full-size image

Figure 4. Probability plot of residuals for specific heat.

To study the effects of combine input variables on the specific heat, 3D surface plots presented in Figure 3 was generated as follows:

Download: Download full-size image

Figure 5. Effect of current and voltage on specific heat.

In other to create a better response, the optimization tool of design expert 13 was employed to optimize the specific heat as presented in Figure 5.

Download: Download full-size image

Figure 6. The Ramp plot for Optimization target of specific heat.

Table 7 presents the effect of the optimization having a desirability of 91.5%. The selected optimal response shows that when a weld parameter of 180amps, 19volts, and 13lit/min is employed to weld a mild steel joint of thickness 10mm using a Tungsten Inert Gas welding process, the specific heat is 445.106j/(Kg°C).

Table 7. The numerical optimal solution.

S/N	I, Amp	E, Volt	GFR (Lmin)	Specific heat J/(Kg°C)
1	180.000	19.000	13.000	445.106
2	179.848	19.000	13.000	444.258
3	180.000	18.987	13.000	444.350
4	180.000	19.000	13.028	444.456
5	180.000	19.000	13.051	443.928
6	180.000	19.000	13.062	443.671
7	179.575	18.991	13.000	442.203
8	179.370	19.000	13.000	441.586
9	180.000	18.959	13.000	442.802
10	180.000	19.000	13.124	442.341
11	180.000	19.000	16.000	475.341
12	179.870	19.000	16.000	474.928
13	180.000	18.929	13.000	441.104
14	180.000	19.000	15.983	474.583
15	180.000	18.983	16.000	474.233
16	179.645	19.000	16.000	474.221
17	180.000	18.967	16.000	473.123
18	179.416	19.000	16.000	473.500

4. Conclusion

This study successfully developed and applied predictive expert models using Response Surface Methodology (RSM) to optimize the specific heat of Tungsten Inert Gas (TIG) welded mild steel (S275). The results demonstrated that welding parameters—namely current, voltage, and shielding gas flow rate—significantly influence the specific heat of the weldments. The RSM-based model showed strong statistical reliability, with high R², Adjusted R², and Predicted R² values, confirming its suitability for modeling and optimization tasks. A second-order quadratic model was established and validated, enabling accurate prediction and optimization of the specific heat response. The optimum process parameters were identified as 180 A welding current, 19 V voltage, and 13 L/min gas flow rate, yielding a specific heat value of 445.106 J/kg°C. Based on the findings, it is recommended that future research explore complementary intelligent modeling techniques—such as Fuzzy Logic Systems and Genetic Algorithms (GA)—to further enhance prediction accuracy and broaden the model’s applicability in different welding conditions.

Abbreviations

ANOVA	Analysis of Variance
CCD	Central Composite Design
DoF	Design of Experiment
GFR	Gas Flow Rate
RSM	Response Surface Methodology
TIG	Tungsten Inert Gas
VIF	Variance Inflation Factor
GA	Genetic Algorithm

Author Contributions

Augustine Oghenekevwe Igbinake is the sole author. The author read and approved the final manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Callister, W. D., & Rethwisch, D. G. (2018). Materials Science and Engineering: An Introduction (10th ed.). Wiley.
[2]	Ferreira, I., Castro, J. A. D., & Garcia, A. (2019). Determination of heat capacity of pure metals, compounds and alloys by analytical and numerical methods. Thermochimica Acta Volume 682, December 2019, 178418.
[3]	Parkinson D. H (1958), The specific heats of metals at low temperatures, Reports on Progress in Physics, Volume 21, Number 1.
[4]	Jones, H. F. (1957). The specific heat of metals and alloys at low temperatures. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences Volume 240, Issue 1222Jun 1957.
[5]	Strombeck, A, Santos, J. F. D., Torster, F. and Koçak, M. (1999) Fracture toughness behavior of FSW joints in aluminium alloys. Proceedings of the I st International Symposium on Friction Stir Welding, 14–16 June, Thousand Oaks, CA, USA.
[6]	Galvao, R. M., Leal, D. M., Rodriguez, and Loureiro, A. (2010). Dissimilar welding of very thin aluminum and copper plates. In Proceedings of the 8th International Friction Stir Welding Symposium. Timmendorfer Strand. pp. 1-8.
[7]	Zhao, Y., Xie, Q., Zhang, J., Liu, X., and Huang, W. (2020) 'Effect of specific heat on the welding distortion of butt-welded joints', Journal of Materials Processing Technology, Vol. 275, pp. 116317.
[8]	Godfrey, S; Tonbra, E (2022), optimization and prediction of melting efficiency of mild steel weldment, using response surface methodology, International Journal of Innovations in Engineering Research and Technology, 9(5), 9. https://doi.org/10.17605/OSF.IO/FEGZY
[9]	Igbinake, A. O (2025) comparison of response surface methodology (RSM) and artificial neural networks (ANN) in optimization of the thermal diffusivity of mild steel TIG welding, American Journal of mechanical and material engineering, 2025, vol. 9, No. 2 pp 43-49.
[10]	Weman, K; (2011), Welding Processes Handbook, 2nd Edition - November 8, 2011.
[11]	Lincoln, E (2014). The Procedure Handbook of Arc Welding 14th ed., page 1.1-1.
[12]	Box, G; Behnken, D, (1960) Some new three level designs for the study of quantitative variables, Technometrics, Volume 2, pages 455–475, 1960.
[13]	Nuran, B. (2007) The Response Surface Methodology. Master of Science in Applied Mathematics and Computer Science, PhD Dissertation, Faculty of the Indiana University, South Bend.
[14]	Sunil C, (2015) ANN and RSM approach for modeling and optimization of designing parameters for a V down perforated baffle roughened rectangular channel Alexandria Engineering Journal Volume 54, Issue 3.

Cite This Article

Plain Text BibTeX RIS

APA Style

Igbinake, A. O. (2025). Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology. Applied Engineering, 9(1), 37-44. https://doi.org/10.11648/j.ae.20250901.13

Copy | Download

ACS Style

Igbinake, A. O. Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology. Appl. Eng. 2025, 9(1), 37-44. doi: 10.11648/j.ae.20250901.13

Copy | Download

AMA Style

Igbinake AO. Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology. Appl Eng. 2025;9(1):37-44. doi: 10.11648/j.ae.20250901.13

Copy | Download

@article{10.11648/j.ae.20250901.13,
  author = {Augustine Oghenekevwe Igbinake},
  title = {Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology
},
  journal = {Applied Engineering},
  volume = {9},
  number = {1},
  pages = {37-44},
  doi = {10.11648/j.ae.20250901.13},
  url = {https://doi.org/10.11648/j.ae.20250901.13},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ae.20250901.13},
  abstract = {Specific heat, an intrinsic thermal property, represents the amount of heat energy required to raise the temperature of a substance by one degree Celsius. Accurate estimation of specific heat in welded metals is crucial for understanding thermal behavior during and after welding processes, especially in applications where temperature control and energy efficiency are essential. This study focuses on the prediction and optimization of the specific heat of mild steel weldments using Response Surface Methodology (RSM), a statistical technique for modeling and analyzing the effects of multiple variables. A total of 100 welded mild steel specimens, each measuring 60 mm × 40 mm × 10 mm, were prepared through controlled Tungsten Inert Gas (TIG) welding operations. During the experiments, key process parameters - welding current, arc voltage, and shielding gas flow rate - were systematically varied to observe their effect on specific heat. The experimental data collected were analyzed using Design Expert 13 software, enabling statistical modeling, regression analysis, and optimization. A second-order quadratic model was developed to describe the relationship between specific heat and the input parameters. The optimal parameter combination was determined to be 180 A, 19 V, and 13 L/min, resulting in a predicted specific heat value of 445.106 J/kg°C. The developed model provides a useful predictive tool for future thermal analysis of welded structures.
},
 year = {2025}
}

Copy | Download

TY  - JOUR
T1  - Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology

AU  - Augustine Oghenekevwe Igbinake
Y1  - 2025/06/04
PY  - 2025
N1  - https://doi.org/10.11648/j.ae.20250901.13
DO  - 10.11648/j.ae.20250901.13
T2  - Applied Engineering
JF  - Applied Engineering
JO  - Applied Engineering
SP  - 37
EP  - 44
PB  - Science Publishing Group
SN  - 2994-7456
UR  - https://doi.org/10.11648/j.ae.20250901.13
AB  - Specific heat, an intrinsic thermal property, represents the amount of heat energy required to raise the temperature of a substance by one degree Celsius. Accurate estimation of specific heat in welded metals is crucial for understanding thermal behavior during and after welding processes, especially in applications where temperature control and energy efficiency are essential. This study focuses on the prediction and optimization of the specific heat of mild steel weldments using Response Surface Methodology (RSM), a statistical technique for modeling and analyzing the effects of multiple variables. A total of 100 welded mild steel specimens, each measuring 60 mm × 40 mm × 10 mm, were prepared through controlled Tungsten Inert Gas (TIG) welding operations. During the experiments, key process parameters - welding current, arc voltage, and shielding gas flow rate - were systematically varied to observe their effect on specific heat. The experimental data collected were analyzed using Design Expert 13 software, enabling statistical modeling, regression analysis, and optimization. A second-order quadratic model was developed to describe the relationship between specific heat and the input parameters. The optimal parameter combination was determined to be 180 A, 19 V, and 13 L/min, resulting in a predicted specific heat value of 445.106 J/kg°C. The developed model provides a useful predictive tool for future thermal analysis of welded structures.

VL  - 9
IS  - 1
ER  -

Copy | Download

Author Information

Augustine Oghenekevwe Igbinake

Department of Production Engineering, University of Benin, Benin City, Nigeria

Contact Email

http://orcid.org/0009-0002-4210-1718

Download PDF

Plain Text BibTeX RIS

APA Style

Igbinake, A. O. (2025). Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology. Applied Engineering, 9(1), 37-44. https://doi.org/10.11648/j.ae.20250901.13

Copy | Download

ACS Style

Igbinake, A. O. Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology. Appl. Eng. 2025, 9(1), 37-44. doi: 10.11648/j.ae.20250901.13

Copy | Download

AMA Style

Igbinake AO. Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology. Appl Eng. 2025;9(1):37-44. doi: 10.11648/j.ae.20250901.13

Copy | Download

@article{10.11648/j.ae.20250901.13,
  author = {Augustine Oghenekevwe Igbinake},
  title = {Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology
},
  journal = {Applied Engineering},
  volume = {9},
  number = {1},
  pages = {37-44},
  doi = {10.11648/j.ae.20250901.13},
  url = {https://doi.org/10.11648/j.ae.20250901.13},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ae.20250901.13},
  abstract = {Specific heat, an intrinsic thermal property, represents the amount of heat energy required to raise the temperature of a substance by one degree Celsius. Accurate estimation of specific heat in welded metals is crucial for understanding thermal behavior during and after welding processes, especially in applications where temperature control and energy efficiency are essential. This study focuses on the prediction and optimization of the specific heat of mild steel weldments using Response Surface Methodology (RSM), a statistical technique for modeling and analyzing the effects of multiple variables. A total of 100 welded mild steel specimens, each measuring 60 mm × 40 mm × 10 mm, were prepared through controlled Tungsten Inert Gas (TIG) welding operations. During the experiments, key process parameters - welding current, arc voltage, and shielding gas flow rate - were systematically varied to observe their effect on specific heat. The experimental data collected were analyzed using Design Expert 13 software, enabling statistical modeling, regression analysis, and optimization. A second-order quadratic model was developed to describe the relationship between specific heat and the input parameters. The optimal parameter combination was determined to be 180 A, 19 V, and 13 L/min, resulting in a predicted specific heat value of 445.106 J/kg°C. The developed model provides a useful predictive tool for future thermal analysis of welded structures.
},
 year = {2025}
}

Copy | Download

TY  - JOUR
T1  - Estimation and Optimization of Specific Heat of TIG Weld of Mild Steel (s275) Using Response Surface Methodology

AU  - Augustine Oghenekevwe Igbinake
Y1  - 2025/06/04
PY  - 2025
N1  - https://doi.org/10.11648/j.ae.20250901.13
DO  - 10.11648/j.ae.20250901.13
T2  - Applied Engineering
JF  - Applied Engineering
JO  - Applied Engineering
SP  - 37
EP  - 44
PB  - Science Publishing Group
SN  - 2994-7456
UR  - https://doi.org/10.11648/j.ae.20250901.13
AB  - Specific heat, an intrinsic thermal property, represents the amount of heat energy required to raise the temperature of a substance by one degree Celsius. Accurate estimation of specific heat in welded metals is crucial for understanding thermal behavior during and after welding processes, especially in applications where temperature control and energy efficiency are essential. This study focuses on the prediction and optimization of the specific heat of mild steel weldments using Response Surface Methodology (RSM), a statistical technique for modeling and analyzing the effects of multiple variables. A total of 100 welded mild steel specimens, each measuring 60 mm × 40 mm × 10 mm, were prepared through controlled Tungsten Inert Gas (TIG) welding operations. During the experiments, key process parameters - welding current, arc voltage, and shielding gas flow rate - were systematically varied to observe their effect on specific heat. The experimental data collected were analyzed using Design Expert 13 software, enabling statistical modeling, regression analysis, and optimization. A second-order quadratic model was developed to describe the relationship between specific heat and the input parameters. The optimal parameter combination was determined to be 180 A, 19 V, and 13 L/min, resulting in a predicted specific heat value of 445.106 J/kg°C. The developed model provides a useful predictive tool for future thermal analysis of welded structures.

VL  - 9
IS  - 1
ER  -

Copy | Download