Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin

Song Wenying; Chen Junbin; Gong Diguang; Wang Xiaoming; Shi Ruidong; Zhang Chengming

doi:doi:10.11648/j.ajce.20251304.13

Research Article |

| Peer-Reviewed

Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin

Song Wenying^*

, Chen Junbin

, Gong Diguang, Wang Xiaoming, Shi Ruidong, Zhang Chengming

Published in American Journal of Civil Engineering (Volume 13, Issue 4)

Received: 3 June 2025 Accepted: 8 July 2025 Published: 23 July 2025

Views: Downloads:

Download PDF

Share This Article

Twitter
Linked In
Facebook

Abstract

Under the geological conditions of sandstone reservoirs in the long 7 sections of Tiezhuizi block, with the increase in the depth of burial and the complexity of geological structure, it leads to the status quo of generally low production capacity of horizontal wells. In the face of this challenge, the optimisation of fracturing engineering desserts is particularly difficult. To cope with this challenge, this study is dedicated to finding a high-precision method for quantitative evaluation of reservoir engineering sweet spots. In this study, principal component analysis was adopted to comprehensively and meticulously analyse nine key engineering sweet spot factors, including core density, elastic modulus, Poisson's ratio, and perimeter pressure. The screening criteria of eigenvalue > 1 accurately identified 2 factors that mainly affect the engineering sweet spot. The cumulative explained variance of these two principal components reaches 91.199 %, which almost covers most of the information. By analysing the positive and negative correlations between the factor loading coefficients of these 2 principal components affecting the engineering sweet spot, these two principal components were identified as the damage resistance factor and the external confining stress factor, respectively. By analysing the rock number composite scores of the principal components, the specific locations of the dominant reservoirs were precisely located, and the dominant reservoirs were located at 2085-2095m, 2035-2045m, 1955-1965m, 1975-1985m and 2005-2015m. This result is more conducive to the realisation of the project, with high accuracy.

Published in	American Journal of Civil Engineering (Volume 13, Issue 4)
DOI	10.11648/j.ajce.20251304.13
Page(s)	211-221
Creative Commons	This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited.
Copyright	Copyright © The Author(s), 2025. Published by Science Publishing Group

Keywords

PCA, Dense Sandstone, Engineering Dessert, Comprehensive Evaluation

1. Introduction

The substantial size of China's onshore oil shale resources and the promising outlook for their exploration and development are well-documented. The presence of favourable conditions conducive to the formation of shale oil in multiple onshore lacustrine formations has been identified in China. Initial estimates suggest that the country's onshore shale oil resources are approximately 1500×10⁸ t, with a recoverable resource estimate ranging from 30 to 60×10⁸ t. In the event of a breakthrough in technology, the potential of the development of shale oil in China is significant in terms of increasing the country's oil and gas reserves. In recent years, the exploration and development of shale oil in the Lower Permian Basin has become a key part of China's energy strategy. The unique physical properties of the reservoir, such as its high-permeability, make it difficult for shale oil to flow naturally, which has an impact on the amount of shale oil produced and the profitability of its extraction. The selection of optimal criteria is a critical step in the development of shale oil in the context of petroleum exploration. By evaluating multiple selection criteria, decision-makers can identify the most suitable option, which provides a scientific basis for the efficient development of resources and the enhancement of efficiency.

The objective of this study is to develop a high-precision quantitative evaluation method for identifying and locating the areas of sandstone reservoirs (particularly the iron-bearing areas of the 7-segment long-term reservoir) where the effects of the hydraulic fracturing have been most effective, i.e. the "engineering sweet spot". This will optimise the hydraulic fracturing design and address the challenges of low productivity caused by increased depth and complex geological structures, thereby enhancing the efficiency of hydraulic fracturing in low-productivity reservoirs.

2. Literature Review

In the field, leading experts from home and abroad have undertaken research projects on the engineering aspects of the project, achieving notable success.

Some scholars comprehensively optimised four engineering sweet spot parameters, namely, brittleness index, stress difference coefficient, fracture toughness, and natural weak surface, and established an engineering sweet spot evaluation method for tight sandstone reservoirs

[1]

. A prediction model for the ‘sweet spot’ of favourable zones of gas reservoirs was put forward, and a quantitative characterization model for the engineering sweet spot of the reservoir was set up to determine the area with the highest development potential

[2]

. A geo-engineering integrated shale gas sweet spot evaluation method based on fuzzy comprehensive evaluation was designed and implemented

[3]

. The quality of hydrocarbon rock, oil content and engineering characteristics of tight oil reservoir were studied. Designed and implemented a geo-engineering integrated shale gas dessert evaluation method based on fuzzy comprehensive evaluation method3; studied the hydrocarbon rock quality, reservoir oil content and engineering characteristics, and established a classification and evaluation system for tight oil ‘desserts’

[4]

. Analysed the lithology of the tight oil desserts from the perspective of geology and engineering, and came up with the optimal exploration and development targets. The geological dessert was analysed in terms of source rock quality, lithological characteristics, reservoir properties and oil content rate. The engineering sweet spot mainly adopts triaxial compression experiment to obtain rock mechanical parameters

[5]

. Later, some scholars proposed a new method of sweet spot evaluation based on fine geological reservoir model, using grey correlation and hierarchical analysis to quantify and characterize the weighting coefficients of each factor, and finally forming the combined weighting coefficient method

[6]

. Based on the established petrophysical relationship, Poisson's ratio and TOC content were further predicted, and the geological sweet spot evaluation of shale oil was realized

[7]

. A novel Convolutional Neural Network (CNN) method is proposed, combining the established CNN model and the micro-migration assessment method to divide four sweet spots

[8]

. A shale oil and gas recoverable reserves prediction model is constructed by using machine learning methods and geological development big data, and the distribution of shale oil and gas recoverable reserves is predicted

[9]

. A new method of reservoir fracturability evaluation based on the logging petrophysical phases clustering analysis is proposed. A new method is proposed to evaluate the fracturability of reservoirs based on logging petrophysical phase cluster analysis. Factors such as rock mechanical characteristics, petrophysical response characteristics, and reservoir physical parameters were comprehensively considered. Using the brittleness index and permeability evaluation index, the fracturability of the reservoir in the target block was classified into five categories, and its fracturability was predicted with an overall prediction accuracy of 81.8%

[10]

. The key parameters affecting the production of horizontal wells were selected, and the weights of these parameters were calculated by fuzzy optimization for quantitative prediction of desserts to establish a sweet spot evaluation system

[11]

. Combined with the observation of thin section and field emission scanning electron microscopy, X-ray diffraction and geochemical indicators, the evaluation system was established to evaluate the fracturability of the reservoir in the target block. diffraction and geochemical indicators, shale reservoir properties were analysed in detail and shale oil sweet spot types were classified, and the distribution pattern of sweet spots was determined, and shale oil geological sweet spots were broadly classified into matrix shale oil, fracture shale oil, interlayer shale oil and composite shale oil types, so that suitable shale oil well locations were determined by searching for geological sweet spots with appropriate organic matter content, interlayer development, light oil and high pressure

[12]

. Six parameters reflecting reservoir quality and completion quality were selected to construct a shale oil horizontal well fracturing dessert evaluation index, and fracturing desserts were classified into Class I (high-quality reservoirs), Class II (secondary reservoirs), and Class III (non-fracturing desserts)

[13]

. Based on the concept of geo-engineering integration, dessert evaluations were carried out to identify brittle, reservoir materiality, and reservoirs with relatively good oil content as horizontal well fracturing targets. Then the UFM model was applied to optimise the fracturing parameters. Based on the concept of geological and engineering integration and taking into account the reservoir quality and engineering quality, the sweet spot evaluation standard of flow two sections was established. Based on the evaluation criteria, four interbedded oil shale reservoir sweet spots were identified

[14]

. Fracturability was defined for the first time, and it was considered that fracturability is the property of shale reservoirs that can be effectively fractured and thus increase production, and that shales with different fracturability form different fracture networks during the hydraulic fracturing process. Fracturability, producibility, and sustainability are key parameters in the evaluation of shale gas wells

[15]

. Combining the brittleness and energy dissipation of shale, a new fracturability index is proposed, which suggests that formations suitable for fracturing are not only brittle, but also require less energy to create new fractures

[16]

. Based on rock mechanics tests and well logs, a prediction model of fracture toughness for gas-bearing shale type I and II was developed and used to predict the fracture toughness of gas-bearing shale. Based on the rock mechanics tests and well logging data, type I and type II fracture toughness prediction models for gas-containing shale were established, and an improved fracturability evaluation model was proposed based on these models, which takes into account the brittleness, fracture toughness, and the minimum horizontal geostress of the shale reservoir

[17]

. A comprehensive multi-scale fracturability evaluation method for dense sandstone reservoirs based on three-dimensional geomechanical analyses has been established. A typical application of the method is to apply the integrated multiscale fracturability evaluation method to tight sandstone reservoirs in the South China Sea oilfields in China, which verifies the validity of the method

[18]

At present, the evaluation of engineering data is typically performed using a variety of methods, including fuzzy c-means clustering, grey relational analysis, and BP neural networks. However, these methods are unable to effectively handle large data sets and accurately identify the significant factors contributing to the engineering data. Principal Component Analysis (PCA) is a statistical technique that is employed to reduce the dimensionality of data sets and identify the principal components that are most relevant to the data. Principal Component Analysis (PCA) is a technique for simplifying data sets. This transformation involves the projection of data onto a new coordinate system, resulting in any data set's Principal Components (PCS) being plotted on the first coordinate system (referred to as the first principal component) and the second coordinate system (referred to as the second principal component), and so on. The primary component analysis typically involves reducing the number of data points while preserving the variability of the data set. This is achieved by focusing on the lower-order components while neglecting the higher-order components. Consequently, the lower-order components are able to capture the most significant aspects of the data. This method has been successfully applied in Y96 well, significantly enhancing the hydraulic fracturing outcomes and demonstrating its applicability in complex geological conditions, thereby providing substantial support for the development of analogous reservoirs.

3. Objective Segmentation and Methods

3.1. Research Zone

The research area is the Erdos Y96 oil reservoir in the Erdos basin, which is located in the northwestern part of China. The Erdos basin is a significant onshore sedimentary basin, and is one of China's primary oil and gas production regions. The Y96 well is located in the primary oil reservoir in the Erdos basin. The Y96 well's reservoir is characterised by high organic content, excellent reservoir quality, and potential for significant oil production. The evaluation of the "desserts" area can improve production efficiency, reduce development costs, optimise resource utilisation, and ensure stable production.

3.2. Data Source

All data presented in this paper is derived from rock samples collected during the drilling process of the Y96 well. The research team has collected data on various aspects, including but not limited to: depth to bottomhole, elastic modulus, pressure collapse, and pressure resistance. The data sources used in this study are listed in Table 1, and include nine parameters: depth to bottomhole, elastic modulus, pressure collapse, pressure resistance, and tensile strength.

3.3. Study Method

The method of analysis employed in this study is the principal component analysis (PCA), a mathematical transformation technique. This technique is employed to analyse a given set of related variables

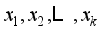, The process of linear transformation results in the conversion of the original set of variables into a new set of variables that are no longer related to each other

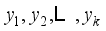, In the context of such transformations, it is imperative to note that （

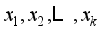） the total variance remains constant.

Concurrently,

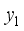possesses the maximum variance and is designated as the primary component;

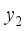possesses the second - largest variance and is designated as the secondary.

Table 1. The following data has been obtained from the Y96 well in the 7th segment of the E'erduosi projectcomponent. In sequence,

components can be derived from

variables, and the variances gradually diminish, becoming independent of the preceding components.

Core number	Burial depth /m	Core densi-ty g/cm³	Poisson ratio	Modulus of elasticity /MPa	Tensile strength /MPa	Compress-ive strength /MPa	Perimeter pressure /MPa	Minimum horizon-tal ground stress /MPa	Maximum horizon-tal ground stress /MPa
1-1	1900	2.659	0.4999890	19336.63	9.67	193.37	19.80	32.18	47.46
1-2	1910	2.625	0.4999852	19066.55	9.53	190.67	19.65	31.94	41.67
1-3	1920	2.624	0.4999858	19062.57	9.53	190.63	19.75	32.09	42.49
1-4	1930	2.612	0.4999861	18977.40	9.49	189.78	19.76	32.11	42.91
1-5	1940	2.66	0.4999872	19332.25	9.67	193.32	20.23	32.87	45.42
1-6	1950	2.626	0.4999884	19092.59	9.55	190.93	20.07	32.62	46.95
1-7	1960	2.702	0.4999871	19636.90	9.82	196.37	20.76	33.74	46.66
1-8	1970	2.638	0.4999862	19166.73	9.58	191.67	20.37	33.10	44.51
1-9	1980	2.684	0.4999875	19509.10	9.75	195.09	20.83	33.85	47.60
1-10	1990	2.589	0.4999858	18808.24	9.40	188.08	20.20	32.82	43.55
1-11	2000	2.565	0.4999861	18635.43	9.32	186.36	20.11	32.68	43.64
1-12	2010	2.627	0.4999836	19071.88	9.54	190.72	20.70	33.64	42.61
1-13	2020	2.55	0.4999868	18530.60	9.27	185.31	20.19	32.81	44.75
1-14	2030	2.594	0.4999861	18846.57	9.42	188.47	20.64	33.54	45.06
1-15	2040	2.648	0.4999851	19233.02	9.62	192.33	21.18	34.41	45.21
1-16	2050	2.544	0.4999914	18516.50	9.26	185.17	20.44	33.22	56.23
1-17	2060	2.447	0.4999906	17804.97	8.90	178.05	19.76	32.11	51.10
1-18	2070	2.325	0.4999930	16933.52	8.47	169.34	18.87	30.66	57.86
1-19	2080	2.559	0.4999896	18613.14	9.31	186.13	20.87	33.91	51.76
1-20	2090	2.627	0.4999869	19090.67	9.55	190.91	21.52	34.97	48.31
1-21	2100	2.567	0.4999900	18674.46	9.34	186.75	21.13	34.34	53.85

In the event of the existence of

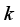samples, each of which contains

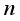indicators, it is possible to construct an

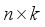data matrix

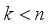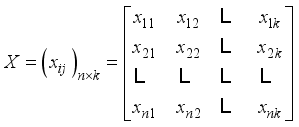(1)

The

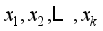are to be defined as the 'original variables'.

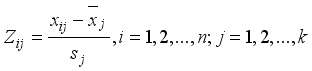A standardisation transformation is applied to the sample matrix：

(2)

where

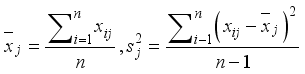, yields the normalized matrix Z.

Find the matrix of correlation coefficients for the normalized matrix Z:

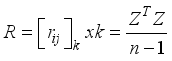(3)

where

Solve the characteristic equation

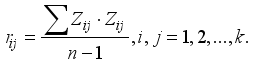
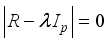for the correlation matrix R to obtain P eigenroots, determine the principal components, for each eigenroot

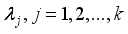such that

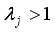Kaiser eigenvalue >1 criterion, determine the value of

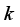. Solve the equation

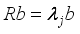to obtain the unit eigenvector

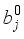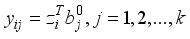Transform standardized indicator variables into principal components

(4)

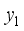is called the first principal component,

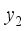is called the second principal component,...,

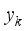is called the

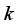th principal component. The weighted summation of the individual principal components yields the final evaluation value, with the weights being the variance contribution ratio of each principal component.

In the actual petroleum exploration and development environment, there are many factors affecting the preferential evaluation of engineering sweetspot, among which there are primary factors and secondary factors, but these factors generally originate from the same general. According to the principle of principal component analysis, the original factors or variables are linearly combined into a number of new variables independent of each other, which is conducive to analyzing the main factors affecting the engineering sweet spot, and then effectively identifying the engineering sweet spot area and making a more accurate exploration and development of the actual program.

4. Integrated Engineering Sweet Spot Evaluation Function

The integrated engineering sweet spot evaluation function was obtained by principal component analysis.

Download: Download full-size image

Figure 1. Process flowchart for the evaluation of sweet points.

Download: Download full-size image

Figure 2. Thermogram of correlation coefficients of various engineering desserts in well Y96.

Table of results of standardisation of engineering dessert data for each well Y96.

X₁Burial depth /m	X₂Core density g/cm³	X₃Poisson ratio	X₄Modulus of elasticity /MPa	X₅Tensile strength /MPa	X₆Compressive strength /MPa	X₇Perimeter pressure /MPa	X₈Minimum horizontal ground stress /MPa	X₉Maximum horizontal ground stress /MPa
-1.611646	0.778566	0.641061	0.806347	0.809657	0.806638	-0.842409	-0.838205	0.073339
-1.450481	0.371912	-0.982960	0.354860	0.341076	0.355233	-1.082989	-1.075140	-1.189730
-1.289317	0.359951	-0.726536	0.348207	0.341076	0.348545	-0.922602	-0.927055	-1.010850
-1.128152	0.216427	-0.598323	0.205830	0.207196	0.206436	-0.906564	-0.907311	-0.919228
-0.966988	0.790526	-0.128212	0.799025	0.809657	0.798279	-0.152749	-0.157016	-0.371680
-0.805823	0.383872	0.384636	0.398391	0.408016	0.398702	-0.409367	-0.403824	-0.037916
-0.644658	1.292864	-0.170950	1.308302	1.311708	1.308200	0.697298	0.701873	-0.101178
-0.483494	0.527397	-0.555586	0.522329	0.508426	0.522420	0.071792	0.070046	-0.570194
-0.322329	1.077576	0.000000	1.094662	1.077417	1.094200	0.809568	0.810468	0.103879
-0.161165	-0.058663	-0.726536	-0.076951	-0.094035	-0.077782	-0.200865	-0.206378	-0.779614
0.000000	-0.345713	-0.598323	-0.365834	-0.361795	-0.365344	-0.345212	-0.344590	-0.759981
0.161165	0.395833	-1.666758	0.363770	0.374546	0.363592	0.601066	0.603150	-0.984672
0.322329	-0.525119	-0.299162	-0.541076	-0.529146	-0.540890	-0.216903	-0.216250	-0.517839
0.483494	0.001139	-0.598323	-0.012876	-0.027095	-0.012579	0.504835	0.504427	-0.450213
0.644658	0.647001	-1.025697	0.633145	0.642306	0.632764	1.370920	1.363317	-0.417491

The above heat map of correlation coefficient matrix shows that 1 means complete positive correlation, -1 means complete negative correlation, and 0 means no linear correlation. It is easy to know that the modulus of elasticity and Poisson's ratio, the peripheral pressure and the depth of burial have strong positive correlation; the compressive strength and the minimum horizontal ground stress, the maximum horizontal ground stress and the depth of burial have strong negative correlation.

Table 3. Explanatory table of total variance for each indicator for well Y96.

Ingredient	The characteristic root value	Variance contribution (%)	Cumulative variance contribution (%)
1	5.84	64.886	64.886
2	2.368	26.313	91.199
3	0.772	8.573	99.772
4	0.02	0.227	99.999
5	/	0.001	100
6	/	/	100
7	/	/	100
8	/	/	100
9	/	/	100

Based on the criterion that the characteristic root is greater than 1 (i.e. Kaiser's criterion)

[19]

, the principal components were quickly screened in the standardised data, and as shown in the above table, there are two principal components with the characteristic root greater than 1, in which the first principal component contributes 64.886% to the total variance of the page, and the cumulative explanation of variance by the two principal components is 91.199%. These two principal components have contained most of the information of the above nine indicators, and their influence on the selection of engineering sweet spot factors is the greatest.

Download: Download full-size image

Figure 3. Gravel diagram.

The gravel plot, i.e. according to the slope of eigenvalue decline and combined with the variance interpretation table can be used to confirm or adjust the number of principal components.

Table of factor loading coefficients.

Title	Principal componentF₁	Principal componentF₂	Commonality (common factor variance)
X₁	-0.52	0.813	0.931
X₂	0.984	0.011	0.968
X₃	-0.783	0.223	0.663
X₄	0.981	0.017	0.962
X₅	0.981	0.016	0.962
X₆	0.981	0.016	0.962
X₇	0.531	0.843	0.992
X₈	0.531	0.843	0.992
X₉	-0.734	0.486	0.776

These two principal components already contain most of the information of the above nine indicators, and their influence on the selection of engineering sweet spot factors is the greatest, and then the first, second, and third principal components are loaded values calculated. The factor loading coefficient measures the strength of correlation between each variable and factor. When the absolute value of the loading coefficient is larger, the higher the degree of correlation between the variable and the factor, the coefficient is close to 1 or -1 means that there is a strong positive or negative relationship between the variable and the factor, and the coefficient is close to 0 means that there is no relationship between the variable and the factor.

Since the loadings of the first principal component on X₁, X₂, X₃, X₄, X₅, X₆, X₇, X₈and X₉ are -0.52, 0.984, -0.783, 0.981, 0.981, 0.981, 0.981, 0.531, 0.531, -0.734, respectively, and the factor loadings of 0.984, 0.981, -0.783, -0.734 The absolute values of these factors are closer to 1, and the corresponding engineering sweet spot factors are core density, Young's modulus, tensile strength, compressive strength, Poisson's ratio, and maximum horizontal principal stress, respectively. It is easy to know that the principal component F₁ has a strong positive correlation with core density, Young's modulus, tensile strength, compressive strength, and a strong negative correlation with Poisson's ratio and maximum horizontal principal stress. This indicates that this core of the Long 7 reservoir has high density, high stiffness, high tensile and compressive strength, low Poisson's ratio (high brittleness), and relatively low horizontal tectonic stress. Taken together, this represents a state of high overall mechanical strength, good stability, and high resistance to deformation and damage of the rock. The analysis shows that the principal component F₁ is the integrated score of the rock samples in the dimension of ‘strength-stiffness-brittleness’, which is the key index to measure the overall ability of the rock to resist deformation and damage. That is, F₁ is the factor of damage resistance.

Similarly, the absolute values of the loading coefficients of the factors 0.813 and 0.843 in the second principal component are closer to 1, and the corresponding engineering sweet spot factors are depth of burial, perimeter pressure, and minimum horizontal ground stress, respectively. depth-induced constraint pressure state. They represent the external loads and constraints acting on the boundaries of the rock units, and F₂ is strongly positively correlated with them, which means that the higher the value of F₂, the higher the depth of the rock environment, the greater the peripheral pressure constraints and the higher the minimum horizontal ground stress. The absolute values of the factor loadings of 0.011, 0.017 and 0.016 are nearly 0, which means that the correlation between the principal component F₂ and core density, Young's modulus, tensile strength and compressive strength is negligible. The core density, Young's modulus, tensile strength and compressive strength are mainly describing the inherent physical and mechanical properties (strength, stiffness and density) of the rock material itself, and F₂ has almost nothing to do with them, which indicates that the F₂ principal component and the damage resistance factor represented by the F₁ principal component are independent of each other. That is, F₂ is the external constraint stress factor.

Table 5. Matrix of principal components (eigenvectors).

Title	Principal Component 1 Vandal Resistance Factor	Principal Component 2 External Constraint Stress Factor
X₁	-0.089	0.343
X₂	0.169	0.005
X₃	-0.134	0.094
X₄	0.168	0.007
X₅	0.168	0.007
X₆	0.168	0.007
X₇	0.091	0.356
X₈	0.091	0.356
X₉	-0.126	0.205

The eigenvectors of the first principal component, i.e., the fragility index, for X₁, X₂, X₃, X₄, X₅, X₆, X₇, X₈and X₉ were calculated to be -0.089, 0.169, -0.134, 0.168, 0.168, 0.168, 0.091, 0.091 and -0.126, The eigenvectors of the second principal component ground stress anisotropy coefficient for X₁, X₂, X₃, X₄, X₅, X₆, X₇, X₈and X₉ are 0.343, 0.005, 0.094, 0.007, 0.007, 0.007, 0.356, 0.356 and 0.205, respectively.

The above eigenvectors illustrate the factor score coefficients (principal component loadings) contained in each component, which are used to compute the component scores to derive the factor formula, which is computed as: linear combination coefficient * (variance explained/cumulative variance explained), and finally normalized to the factor weight scores.

According to the principal component eigenvectors, the linear relationship between each index and the principal component damage resistance factor F₁ and external constraint stress factor F₂ is derived as:

F₁=-0.089X₁+0.169X₂-0.134X₃+0.168X₄+0.168X₅+0.168X₆+0.091X₇+0.091X₈-0.126X₉

F₂=0.343X₁+0.005X₂+0.094X₃+0.007X₄+0.007X₅+0.007X₆+0.356X₇+0.356X₈+0.205X₉

From the above, we can get the comprehensive evaluation function of the engineering sweet spot of the Y96 well in the long 7 section:

F=(0.649/0.912)×F₁+(0.263/0.912)×F₂

Table 6. Factor weighting analysis table.

title	variance explained rate (%)	Cumulative variance explained (%)	Weights (%)
Vandal Resistance Factor F₁	0.649	64.886	71.147
External Constraint Stress FactorF₂	0.263	91.199	28.853

From the weight calculation results of the principal component analysis in the above table, it can be seen that the weight of the anti-destructive capacity factor is 71.147%, and the weight of the external constraint stress factor is 28.853%, in which the maximum value of the indicator's weight is the anti-destructive capacity factor (71.147%), and the minimum value is the external constraint stress factor (28.853%).

While the engineering sweet spot comprehensive evaluation function F is a comprehensive index for evaluating the reservoir transformation potential, the weight indicates that the damage resistance capacity (F₁) has the greatest influence on the results, followed by the external constraint stress factor.

Based on the known engineering dessert comprehensive evaluation function of some well sections of Y96 wells in the long section 7, the comprehensive scoring table of the reservoir where each rock is located at different depths is calculated and sequentially sorted, as shown in Table 7.

Table 7. Fracturability scores of reservoirs hosting individual rocks at different depths.

Rank	Rock number	Fracturability score	Vandal Resistance Factor	External Constraint Stress Factor
1	1-20	0.897	0.489	1.902
2	1-15	0.87	0.807	1.026
3	1-7	0.859	1.098	0.27
4	1-9	0.785	0.893	0.519
5	1-12	0.531	0.694	0.13
6	1-5	0.321	0.659	-0.512
7	1-8	0.316	0.553	-0.268
8	1-14	0.236	0.177	0.38
9	1-21	0.223	-0.444	1.869
10	1-19	0.047	-0.477	1.339
11	1-1	0.005	0.434	-1.053
12	1-6	0.003	0.219	-0.528
13	1-10	-0.037	0.124	-0.434
14	1-3	-0.105	0.407	-1.367
15	1-2	-0.136	0.454	-1.591
16	1-4	-0.175	0.269	-1.269
17	1-11	-0.226	-0.128	-0.470
18	1-13	-0.285	-0.323	-0.191
19	1-16	-0.360	-0.896	0.962
20	1-17	-1.237	-1.716	-0.056
21	1-18	-2.535	-3.296	-0.658

It is easy to know that 1-20, 1-15, 1-7, 1-9, 1-12 have a composite score >0.5, and their corresponding burial depths are 2090m, 2040m, 1960m, 1980m, 2010m, 1940m, 1970m, 2030m, which can be extended up and down by 5m in the practical application of the project and uniformly regarded as 2085-2095m, and the rest of them are the same. For 2035~2045m, 1955~1965m, 1975~1985m and 2005~2015m, the explanation of the reservoir section is the dominant reservoir.

5. Conclusion

1) By analysing 9 engineering dessert factors through principal component analysis, 2 main factors affecting engineering desserts were selected by using their eigenvalues > 1. The cumulative explained variance of these 2 principal components reaches 91.199%, which can explain most of the information.

2) By analysing the positive and negative correlation between the factor loading coefficients of these 2 main components affecting the engineering sweet spot, it is easy to know that these two main components are the anti-destructive capacity factor and the external constraint stress factor, and then F is used as a comprehensive index for evaluating the transformation potential of the reservoir.

3) Using the principal component analysis method, it is known that when the burial depth is about 2085-2095m, 2035-2045m, 1955-1965m, 1975-1985m and 2005-2015m, the reservoir is the dominant reservoir. This result is more conducive to the realisation of the project, with high accuracy.

Abbreviations

TOC	Total Organic Carbon
CNN	Convolutional Neural Network
PCA	Principal Component Analysis
PCS	Principal Components

Acknowledgments

Supported by National Natural Science Foundation of China "Research on the Evolution Mechanism and Effectiveness Evaluation of Closely Cut Volume Fracture Networks in Onshore Shale Oil Reservoirs" (No. 52274040).

Author Contributions

Wenying Song: Conceptualization, Resources, Data curation, Software, Writing – review & editing

Junbin Chen: Data curation, Funding acquisition, Methodology, Investigation, Validation, Supervision

Diguang Gong: Supervision, Investigation, Visualization, Methodology

Xiaoming Wang: Investigation, Visualization, Software, Investigation, Writing – original draft

Ruidong Shi: Formal Analysis, Visualization, Investigation, Project administration

Chengming Zhang: Formal Analysis, Investigation, Software, Project administration

Funding

This work is supported by the National Natural Science Foundation of China (Grant No. 52274040).

Data Availability Statement

The data supporting the outcome of this research work has been reported in this manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Bai X, Li Z, Lai F, et al. Method for evaluation of engineering sweet spots tight sandstone reservoir production wells [J]. Arabian Journal of Geosciences, 2021, 14(24): 1-12. https://doi.org/10.1007/s12517-021-09216-3
[2]	Liu Z, Tang X, Liu H, et al. Predicting the engineering sweet spot of coal-bed methane reservoirs: a case study from Central China [J]. Arabian Journal of Geosciences, 2022, 15(7): 1-9. https://doi.org/10.1007/s12517-022-09751-7
[3]	Liu S, Liu Y, Zhang X, et al. Geological and Engineering Integrated Shale Gas Sweet Spots Evaluation Based on Fuzzy Comprehensive Evaluation Method: A Case Study of Z Shale Gas Field HB Block [J]. Energies, 2022, 15. https://doi.org/10.3390/en15020602
[4]	Qiu X, Zhang J, Lei H, et al. Comprehensive evaluation of geology-engineering “sweet spot” of tight oil reservoir in Maling Area, Ordos Basin, China [J]. Carbonates and Evaporites, 2025, 40(1). https://doi.org/10.1007/s13146-024-01002-y
[5]	Guo D, Zhang L, Ma B, et al. Dessert Lithofacies Study of Fengxi Tight Oil in Qaidam Basin [J]. Journal of Physics: Conference Series, 2024, 2834(1). https://doi.org/10.1088/1742-6596/2834/1/012055
[6]	Jiang M, Peng C, Wu J, et al. A New Approach to a Fracturing Sweet Spot Evaluation Method Based on Combined Weight Coefficient Method—A Case Study in the BZ Oilfield, China [J]. Processes, 2024, 12(9). https://doi.org/10.3390/pr12091830
[7]	Yu Z, Ma S, Mallick S, et al. Prediction of shale oil “sweet spot” parameters centered on seismic prestack waveform inversion [J]. Geoenergy Science and Engineering, 2024, 241(000): 11. https://doi.org/10.1016/j.geoen.2024.213157.
[8]	Wu Y, Jiang F, Hu T, et al. Shale oil content evaluation and sweet spot prediction based on convolutional neural network [J]. Marine and Petroleum Geology, 2024, 167(000): 15. https://doi.org/10.1016/j.marpetgeo.2024.106997.
[9]	Wang H, Guo Z, Kong X, et al. Application of Machine Learning for Shale Oil and Gas “Sweet Spots” Prediction [J]. Energies, 2024, 17(9): 2191. https://doi.org/10.3390/en17092191
[10]	Xiao Z, Jianguang W, Xiaofeng Z, et al. A New Method for Evaluating Fracability Based on Cluster Analysis and Well Logging Petrophysical Facies Division [J]. Journal of Physics: Conference Series, 2023, 2610(1). https://doi.org/10.1088/1742-6596/2610/1/012035
[11]	Zeng Q, Chen S, He P, et al. Quantitative prediction of shale gas sweet spots based on seismic data in Lower Silurian Longmaxi Formation, Weiyuan area, Sichuan Basin, SW China [J]. Petroleum Exploration and Development Online, 2018, 45(3): 422-430. https://doi.org/10.1016/S1876-3804(18)30047-8
[12]	Zhang S, Liu H, Liu Y, et al. Main controls and geological sweet spot types in Paleogene shale oil rich areas of the Jiyang Depression, Bohai Bay basin, China [J]. Marine and Petroleum Geology, 2020, 111, 576-587. https://doi.org/10.1016/j.marpetgeo.2019.08.054
[13]	Liu Z, Xie Z, Wang C X, et al. Preferred Selection of Fractured Sweet Spot Section for Horizontal Shale Oil Well in West 233 Area [C]. Journal of Physics: Conference Series. IOP Publishing, 2023, 2563(1): 012-036. https://doi.org/10.1088/1742-6596/2563/1/012036
[14]	Shen Y, Liu B, Jiang H, et al. Geological and Engineering Integration Fracturing Design and Optimization Study of Liushagang Formation in Weixinan Sag [J]. Journal of Marine Science and Engineering, 2024, 12(10): 1821. https://doi.org/10.3390/jmse12101821
[15]	Chong K K, Grieser W V, Passman A, et al. A completions guide book to shale-play development: a review of successful approaches toward shale-play stimulation in the last two decades [C]. SPE Canadian Unconventional Resources and International Petroleum Conference, Calgary, Alberta, Canada, 2010. https://doi.org/10.2118/133874-MS
[16]	Jin X, Shah S N, Roegiers J C, et al. Fracability evaluation in shale reservoirs-an integrated petrophysics and geomechanics approach [C]. SPE Hydraulic Fracturing Technology Conference, The Woodlands, Texas, USA, 2014. https://doi.org/10.2118/168589-MS
[17]	Yuan J, Zhou J, Liu S, et al. An improved fracability-evaluation method for shale reservoirs based on new fracture toughness-prediction models. SPE Journal, 2017, 22(05), 1704-1713. https://doi.org/10.2118/185963-PA
[18]	Peng C Y, Liu W J, Huang Z X, et al. An integrated multi-scale fracability evaluation method for tight sandstone reservoir [C]. ISRM International Symposium-Asian Rock Mechanics Symposium. ISRM, 2021: ISRM-ARMS11-2021-322. https://doi.org/10.1088/1755-1315/861/6/062072
[19]	Kaiser, Henry F. The application of electronic computers to factor analysis."Educational and psychological measurement, 20.1 (1960): 141-151. http://dx.doi.org/10.1177/001316446002000116

Cite This Article

Plain Text BibTeX RIS

APA Style

Wenying, S., Junbin, C., Diguang, G., Xiaoming, W., Ruidong, S., et al. (2025). Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin. American Journal of Civil Engineering, 13(4), 211-221. https://doi.org/10.11648/j.ajce.20251304.13

Copy | Download

ACS Style

Wenying, S.; Junbin, C.; Diguang, G.; Xiaoming, W.; Ruidong, S., et al. Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin. Am. J. Civ. Eng. 2025, 13(4), 211-221. doi: 10.11648/j.ajce.20251304.13

Copy | Download

AMA Style

Wenying S, Junbin C, Diguang G, Xiaoming W, Ruidong S, et al. Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin. Am J Civ Eng. 2025;13(4):211-221. doi: 10.11648/j.ajce.20251304.13

Copy | Download

@article{10.11648/j.ajce.20251304.13,
  author = {Song Wenying and Chen Junbin and Gong Diguang and Wang Xiaoming and Shi Ruidong and Zhang Chengming},
  title = {Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin
},
  journal = {American Journal of Civil Engineering},
  volume = {13},
  number = {4},
  pages = {211-221},
  doi = {10.11648/j.ajce.20251304.13},
  url = {https://doi.org/10.11648/j.ajce.20251304.13},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajce.20251304.13},
  abstract = {Under the geological conditions of sandstone reservoirs in the long 7 sections of Tiezhuizi block, with the increase in the depth of burial and the complexity of geological structure, it leads to the status quo of generally low production capacity of horizontal wells. In the face of this challenge, the optimisation of fracturing engineering desserts is particularly difficult. To cope with this challenge, this study is dedicated to finding a high-precision method for quantitative evaluation of reservoir engineering sweet spots. In this study, principal component analysis was adopted to comprehensively and meticulously analyse nine key engineering sweet spot factors, including core density, elastic modulus, Poisson's ratio, and perimeter pressure. The screening criteria of eigenvalue > 1 accurately identified 2 factors that mainly affect the engineering sweet spot. The cumulative explained variance of these two principal components reaches 91.199 %, which almost covers most of the information. By analysing the positive and negative correlations between the factor loading coefficients of these 2 principal components affecting the engineering sweet spot, these two principal components were identified as the damage resistance factor and the external confining stress factor, respectively. By analysing the rock number composite scores of the principal components, the specific locations of the dominant reservoirs were precisely located, and the dominant reservoirs were located at 2085-2095m, 2035-2045m, 1955-1965m, 1975-1985m and 2005-2015m. This result is more conducive to the realisation of the project, with high accuracy.},
 year = {2025}
}

Copy | Download

TY  - JOUR
T1  - Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin

AU  - Song Wenying
AU  - Chen Junbin
AU  - Gong Diguang
AU  - Wang Xiaoming
AU  - Shi Ruidong
AU  - Zhang Chengming
Y1  - 2025/07/23
PY  - 2025
N1  - https://doi.org/10.11648/j.ajce.20251304.13
DO  - 10.11648/j.ajce.20251304.13
T2  - American Journal of Civil Engineering
JF  - American Journal of Civil Engineering
JO  - American Journal of Civil Engineering
SP  - 211
EP  - 221
PB  - Science Publishing Group
SN  - 2330-8737
UR  - https://doi.org/10.11648/j.ajce.20251304.13
AB  - Under the geological conditions of sandstone reservoirs in the long 7 sections of Tiezhuizi block, with the increase in the depth of burial and the complexity of geological structure, it leads to the status quo of generally low production capacity of horizontal wells. In the face of this challenge, the optimisation of fracturing engineering desserts is particularly difficult. To cope with this challenge, this study is dedicated to finding a high-precision method for quantitative evaluation of reservoir engineering sweet spots. In this study, principal component analysis was adopted to comprehensively and meticulously analyse nine key engineering sweet spot factors, including core density, elastic modulus, Poisson's ratio, and perimeter pressure. The screening criteria of eigenvalue > 1 accurately identified 2 factors that mainly affect the engineering sweet spot. The cumulative explained variance of these two principal components reaches 91.199 %, which almost covers most of the information. By analysing the positive and negative correlations between the factor loading coefficients of these 2 principal components affecting the engineering sweet spot, these two principal components were identified as the damage resistance factor and the external confining stress factor, respectively. By analysing the rock number composite scores of the principal components, the specific locations of the dominant reservoirs were precisely located, and the dominant reservoirs were located at 2085-2095m, 2035-2045m, 1955-1965m, 1975-1985m and 2005-2015m. This result is more conducive to the realisation of the project, with high accuracy.
VL  - 13
IS  - 4
ER  -

Copy | Download

Author Information

Song Wenying

College of Petroleum Engineering, Xi'an Shiyou University, Xi'an, China. College of Petroleum Engineering and The Key Laboratory of Well Stability and Fluid & Rock Mechanics in Oil and Gas Reservoirs, Xi'an Shiyou University, Xi'an, China

Contact Email

http://orcid.org/0009-0005-3551-5180
Chen Junbin

College of Petroleum Engineering, Xi'an Shiyou University, Xi'an, China. College of Petroleum Engineering and The Key Laboratory of Well Stability and Fluid & Rock Mechanics in Oil and Gas Reservoirs, Xi'an Shiyou University, Xi'an, China

Contact Email

http://orcid.org/0009-0001-1766-9427
Gong Diguang

College of Petroleum Engineering, Xi'an Shiyou University, Xi'an, China. College of Petroleum Engineering and The Key Laboratory of Well Stability and Fluid & Rock Mechanics in Oil and Gas Reservoirs, Xi'an Shiyou University, Xi'an, China

Contact Email
Wang Xiaoming

College of Petroleum Engineering, Xi'an Shiyou University, Xi'an, China. College of Petroleum Engineering and The Key Laboratory of Well Stability and Fluid & Rock Mechanics in Oil and Gas Reservoirs, Xi'an Shiyou University, Xi'an, China

Contact Email
Shi Ruidong

College of Petroleum Engineering, Xi'an Shiyou University, Xi'an, China. College of Petroleum Engineering and The Key Laboratory of Well Stability and Fluid & Rock Mechanics in Oil and Gas Reservoirs, Xi'an Shiyou University, Xi'an, China

Contact Email
Zhang Chengming

College of Petroleum Engineering, Xi'an Shiyou University, Xi'an, China. College of Petroleum Engineering and The Key Laboratory of Well Stability and Fluid & Rock Mechanics in Oil and Gas Reservoirs, Xi'an Shiyou University, Xi'an, China

Contact Email

Download PDF

Submit an Article

Plain Text BibTeX RIS

APA Style

Wenying, S., Junbin, C., Diguang, G., Xiaoming, W., Ruidong, S., et al. (2025). Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin. American Journal of Civil Engineering, 13(4), 211-221. https://doi.org/10.11648/j.ajce.20251304.13

Copy | Download

ACS Style

Wenying, S.; Junbin, C.; Diguang, G.; Xiaoming, W.; Ruidong, S., et al. Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin. Am. J. Civ. Eng. 2025, 13(4), 211-221. doi: 10.11648/j.ajce.20251304.13

Copy | Download

AMA Style

Wenying S, Junbin C, Diguang G, Xiaoming W, Ruidong S, et al. Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin. Am J Civ Eng. 2025;13(4):211-221. doi: 10.11648/j.ajce.20251304.13

Copy | Download

@article{10.11648/j.ajce.20251304.13,
  author = {Song Wenying and Chen Junbin and Gong Diguang and Wang Xiaoming and Shi Ruidong and Zhang Chengming},
  title = {Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin
},
  journal = {American Journal of Civil Engineering},
  volume = {13},
  number = {4},
  pages = {211-221},
  doi = {10.11648/j.ajce.20251304.13},
  url = {https://doi.org/10.11648/j.ajce.20251304.13},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajce.20251304.13},
  abstract = {Under the geological conditions of sandstone reservoirs in the long 7 sections of Tiezhuizi block, with the increase in the depth of burial and the complexity of geological structure, it leads to the status quo of generally low production capacity of horizontal wells. In the face of this challenge, the optimisation of fracturing engineering desserts is particularly difficult. To cope with this challenge, this study is dedicated to finding a high-precision method for quantitative evaluation of reservoir engineering sweet spots. In this study, principal component analysis was adopted to comprehensively and meticulously analyse nine key engineering sweet spot factors, including core density, elastic modulus, Poisson's ratio, and perimeter pressure. The screening criteria of eigenvalue > 1 accurately identified 2 factors that mainly affect the engineering sweet spot. The cumulative explained variance of these two principal components reaches 91.199 %, which almost covers most of the information. By analysing the positive and negative correlations between the factor loading coefficients of these 2 principal components affecting the engineering sweet spot, these two principal components were identified as the damage resistance factor and the external confining stress factor, respectively. By analysing the rock number composite scores of the principal components, the specific locations of the dominant reservoirs were precisely located, and the dominant reservoirs were located at 2085-2095m, 2035-2045m, 1955-1965m, 1975-1985m and 2005-2015m. This result is more conducive to the realisation of the project, with high accuracy.},
 year = {2025}
}

Copy | Download

TY  - JOUR
T1  - Comprehensive Evaluation of PCA-based Engineering Sweet Spot Logging in Tight Sandstone Reservoirs -- Example of Y96 Well in Long 7 Section of Tiezhuzi Block in Ordos Basin

AU  - Song Wenying
AU  - Chen Junbin
AU  - Gong Diguang
AU  - Wang Xiaoming
AU  - Shi Ruidong
AU  - Zhang Chengming
Y1  - 2025/07/23
PY  - 2025
N1  - https://doi.org/10.11648/j.ajce.20251304.13
DO  - 10.11648/j.ajce.20251304.13
T2  - American Journal of Civil Engineering
JF  - American Journal of Civil Engineering
JO  - American Journal of Civil Engineering
SP  - 211
EP  - 221
PB  - Science Publishing Group
SN  - 2330-8737
UR  - https://doi.org/10.11648/j.ajce.20251304.13
AB  - Under the geological conditions of sandstone reservoirs in the long 7 sections of Tiezhuizi block, with the increase in the depth of burial and the complexity of geological structure, it leads to the status quo of generally low production capacity of horizontal wells. In the face of this challenge, the optimisation of fracturing engineering desserts is particularly difficult. To cope with this challenge, this study is dedicated to finding a high-precision method for quantitative evaluation of reservoir engineering sweet spots. In this study, principal component analysis was adopted to comprehensively and meticulously analyse nine key engineering sweet spot factors, including core density, elastic modulus, Poisson's ratio, and perimeter pressure. The screening criteria of eigenvalue > 1 accurately identified 2 factors that mainly affect the engineering sweet spot. The cumulative explained variance of these two principal components reaches 91.199 %, which almost covers most of the information. By analysing the positive and negative correlations between the factor loading coefficients of these 2 principal components affecting the engineering sweet spot, these two principal components were identified as the damage resistance factor and the external confining stress factor, respectively. By analysing the rock number composite scores of the principal components, the specific locations of the dominant reservoirs were precisely located, and the dominant reservoirs were located at 2085-2095m, 2035-2045m, 1955-1965m, 1975-1985m and 2005-2015m. This result is more conducive to the realisation of the project, with high accuracy.
VL  - 13
IS  - 4
ER  -

Copy | Download