Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport

Kwang-Ok Ri; Yong-Ho Kim; Chol-U Kim; Jong-Chol Paek; Song-Chol Hong

doi:doi:10.11648/j.ijamtp.20251102.11

Research Article |

| Peer-Reviewed

Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport

Kwang-Ok Ri

, Yong-Ho Kim^*

, Chol-U Kim

, Jong-Chol Paek

, Song-Chol Hong

Published in International Journal of Applied Mathematics and Theoretical Physics (Volume 11, Issue 2)

Received: 21 February 2025 Accepted: 9 May 2025 Published: 21 June 2025

Views: Downloads:

Download PDF

Share This Article

Twitter
Linked In
Facebook

Abstract

In this paper, we study the following chemotaxis-Stokes system with active transport 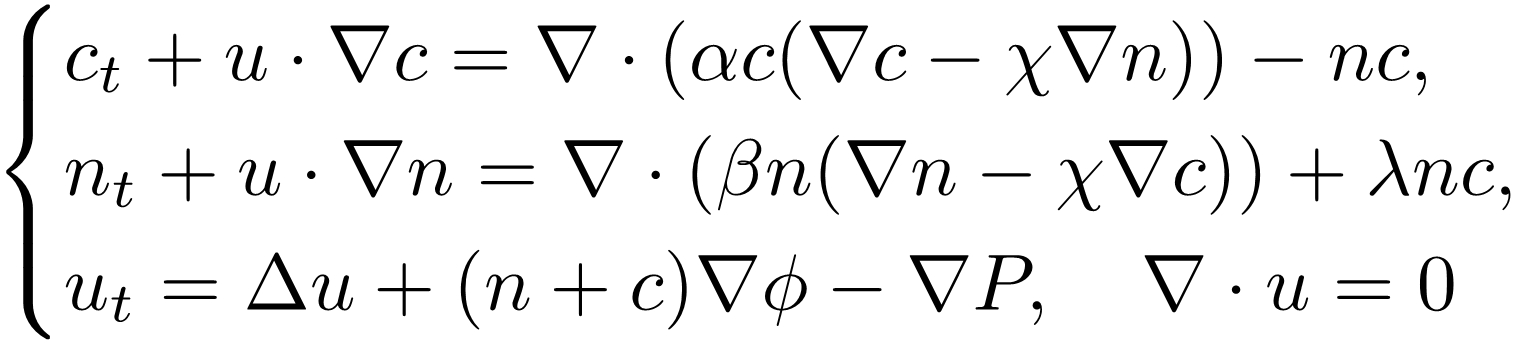in a bounded domain with positive parameters α, β, χ and λ. Here, c and n denote the density of the nutrient acting as a chemoattractant and the density of the cell, respectively and u denotes the velocity of the fluid. The parameters α, β, χ and λ are positive constants and λ represents the cell growth rate occurred by the nutrient supply. The novelty of this system is that there is not only a chemotaxis term, which reflects the movement of the cells toward nutrient sources, but also an active transport one, which means the nutrient is moving towards the cells. In order to prove the existence of weak solutions to the above problem, we introduce the regularized problem using the the Yosida approximation of B := −∆ + 1 under homogeneous Neumann boundary conditions in L² (Ω). Based on a priori estimates for the solutions of the regularized problem, it is shown that under no-flux boundary condition and for any suitably regular initial data, an associated initial value problem possesses a global weak solution provided 0 < χ < 1.

Published in	International Journal of Applied Mathematics and Theoretical Physics (Volume 11, Issue 2)
DOI	10.11648/j.ijamtp.20251102.11
Page(s)	24-30
Creative Commons	This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited.
Copyright	Copyright © The Author(s), 2025. Published by Science Publishing Group

Keywords

Chemotaxis-Stokes, Active Transport, Weak Solution

References

[1]	E. Keller, L. Segel, Model for chemotaxis, J. Theor. Biol. 30 (1979) 225–234.
[2]	T. Hillen, K. Painter, A user’s guide to PDE models for chemotaxis, J. Math. Biol. 58 (2009) 183–217.
[3]	T. Nagai, Blow-up of radially symmetric solutions to a chemotaxis system, Adv. Math. Sci. Appl. 5 (1995) 581–601.
[4]	M. Winkler, Aggregation vs. global diffusive behavior in the higher-dimensional Keller-Segel model, J. Differential Equations 248 (2010) 2889–2905.
[5]	N. Mizoguchi, P. Souplet, Nondegeneracy of blow-up points for the parabolic Keller-Segel system, Ann. Inst. H. Poincaé Anal. Non Linéaire 31 (2014) 851–875.
[6]	N. Bellomo, A. Bellouquid, Y. Tao, M. Winker, Toward a mathematical theory of Keller-Segel models of pattern formation in biological tissues, Math. Models Methods Appl. Sci. 25 (2015) 1663–1763.
[7]	Y.Wang, M.Winkler, Z.Xiang, Globalclassicalsolutions in a two-dimensional chemotaxis-Navier-Stokes system with subcritical sensitivity, Annali della Scuola Normale Superiore di Pisa-Classe di Scienze XVIII (2018) 2036– 2145.
[8]	A. Khelghati, K. Baghaei, Boundedness of classical solutions for a chemotaxis model with rotational flux terms, Z. Agew. Math. Mech 98 (2018) 1864–1877.
[9]	Q. Zhang, W. Tao, Bounedness and stabilization in a two-species chemotaxis system with signal absorption, Computers and Mathematics with Applications 78 (2019) 2672–2681.
[10]	K. Nam, K. Li, Y. Kim, Boundedness of solutions to a 2D chemotaxis-Navier-Stokes system with general sensitivity and nonlinear diffusion, Nonlinear Anal. RWA 73 (2023) 103906.
[11]	Y. Kim, K. Li, K. Nam, Global solvability and stabilization in a three-dimensional coral fertilization model involving the Navier-Stokes equations, J. Math. Anal. Appl. 534 (2024) 128048.
[12]	H. Garcke, K. Lam, E. Sitka, V. Styles, A Cahn-Hilliard- Darcy model for tumour growth with chemotaxis and active transport, Math. Models Methods Appl. Sci. 26 (2016) 1095–1148.
[13]	H. Garcke, K. Lam, Analysis of a Cahn-Hilliard system with non-zero Dirichlet conditions modeling tumor growth with chemotaxis, Discrete Contin. Dyn. Syst. 37 (2017) 4277–4308.
[14]	H. Garcke, K. Lam, Well-posedness of a Cahn-Hilliard system modelling tumour growth with chemotaxis and active transport, European J. Appl. Math. 28(2) (2017) 284–316.
[15]	M. Ebenbeck, H. Garcke, Analysis of a Cahn-Hilliard- Brinkman model for tumour growth with chemotaxis, J. Differential Equations 266(9) (2019) 5998–6036.
[16]	Y. Tao, M. Winkler, A chemotaxis-haptotaxis model: The roles of nonlinear diffusion and logistic source, SIAM J. Math. Anal. 43 (2011) 685–704.
[17]	M. Winkler, A three-dimensional Keller-Segel-Navier- Stokes system with logistic source: Global weak solutions and asymptotic stabilization, J. Functional Analysis 276 (2019) 1339–1401.

Cite This Article

Plain Text BibTeX RIS

APA Style

Ri, K., Kim, Y., Kim, C., Paek, J., Hong, S. (2025). Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport. International Journal of Applied Mathematics and Theoretical Physics, 11(2), 24-30. https://doi.org/10.11648/j.ijamtp.20251102.11

Copy | Download

ACS Style

Ri, K.; Kim, Y.; Kim, C.; Paek, J.; Hong, S. Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport. Int. J. Appl. Math. Theor. Phys. 2025, 11(2), 24-30. doi: 10.11648/j.ijamtp.20251102.11

Copy | Download

AMA Style

Ri K, Kim Y, Kim C, Paek J, Hong S. Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport. Int J Appl Math Theor Phys. 2025;11(2):24-30. doi: 10.11648/j.ijamtp.20251102.11

Copy | Download

@article{10.11648/j.ijamtp.20251102.11,
  author = {Kwang-Ok Ri and Yong-Ho Kim and Chol-U Kim and Jong-Chol Paek and Song-Chol Hong},
  title = {Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport},
  journal = {International Journal of Applied Mathematics and Theoretical Physics},
  volume = {11},
  number = {2},
  pages = {24-30},
  doi = {10.11648/j.ijamtp.20251102.11},
  url = {https://doi.org/10.11648/j.ijamtp.20251102.11},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijamtp.20251102.11},
  abstract = {In this paper, we study the following chemotaxis-Stokes system with active transport  in a bounded domain with positive parameters α, β, χ and λ. Here, c and n denote the density of the nutrient acting as a chemoattractant and the density of the cell, respectively and u denotes the velocity of the fluid. The parameters α, β, χ and λ are positive constants and λ represents the cell growth rate occurred by the nutrient supply. The novelty of this system is that there is not only a chemotaxis term, which reflects the movement of the cells toward nutrient sources, but also an active transport one, which means the nutrient is moving towards the cells. In order to prove the existence of weak solutions to the above problem, we introduce the regularized problem using the the Yosida approximation of B := −∆ + 1 under homogeneous Neumann boundary conditions in L2 (Ω). Based on a priori estimates for the solutions of the regularized problem, it is shown that under no-flux boundary condition and for any suitably regular initial data, an associated initial value problem possesses a global weak solution provided 0 χ < 1.},
 year = {2025}
}

Copy | Download

TY  - JOUR
T1  - Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport
AU  - Kwang-Ok Ri
AU  - Yong-Ho Kim
AU  - Chol-U Kim
AU  - Jong-Chol Paek
AU  - Song-Chol Hong
Y1  - 2025/06/21
PY  - 2025
N1  - https://doi.org/10.11648/j.ijamtp.20251102.11
DO  - 10.11648/j.ijamtp.20251102.11
T2  - International Journal of Applied Mathematics and Theoretical Physics
JF  - International Journal of Applied Mathematics and Theoretical Physics
JO  - International Journal of Applied Mathematics and Theoretical Physics
SP  - 24
EP  - 30
PB  - Science Publishing Group
SN  - 2575-5927
UR  - https://doi.org/10.11648/j.ijamtp.20251102.11
AB  - In this paper, we study the following chemotaxis-Stokes system with active transport  in a bounded domain with positive parameters α, β, χ and λ. Here, c and n denote the density of the nutrient acting as a chemoattractant and the density of the cell, respectively and u denotes the velocity of the fluid. The parameters α, β, χ and λ are positive constants and λ represents the cell growth rate occurred by the nutrient supply. The novelty of this system is that there is not only a chemotaxis term, which reflects the movement of the cells toward nutrient sources, but also an active transport one, which means the nutrient is moving towards the cells. In order to prove the existence of weak solutions to the above problem, we introduce the regularized problem using the the Yosida approximation of B := −∆ + 1 under homogeneous Neumann boundary conditions in L2 (Ω). Based on a priori estimates for the solutions of the regularized problem, it is shown that under no-flux boundary condition and for any suitably regular initial data, an associated initial value problem possesses a global weak solution provided 0 χ < 1.
VL  - 11
IS  - 2
ER  -

Copy | Download

Author Information

Kwang-Ok Ri

Department of Mathematics, University of Sciences, Pyongyang, DPR Korea

Contact Email

http://orcid.org/0009-0005-4745-1938
Yong-Ho Kim

Department of Mathematics, University of Sciences, Pyongyang, DPR Korea

Contact Email

http://orcid.org/0000-0001-5362-128X
Chol-U Kim

Institute of Information Technology, University of Sciences, Pyongyang, DPR Korea

Contact Email

http://orcid.org/0009-0003-9000-5728
Jong-Chol Paek

Department of Environmental Science, Phyongsong University of Education, Phyongsong, DPR Korea

Contact Email

http://orcid.org/0009-0007-4892-6987
Song-Chol Hong

Department of Mathematics, KimJongSuk University of Education, Hyesan, DPR Korea

Contact Email

http://orcid.org/0009-0008-1980-7134

Download PDF

Sections

Plain Text BibTeX RIS

APA Style

Ri, K., Kim, Y., Kim, C., Paek, J., Hong, S. (2025). Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport. International Journal of Applied Mathematics and Theoretical Physics, 11(2), 24-30. https://doi.org/10.11648/j.ijamtp.20251102.11

Copy | Download

ACS Style

Ri, K.; Kim, Y.; Kim, C.; Paek, J.; Hong, S. Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport. Int. J. Appl. Math. Theor. Phys. 2025, 11(2), 24-30. doi: 10.11648/j.ijamtp.20251102.11

Copy | Download

AMA Style

Ri K, Kim Y, Kim C, Paek J, Hong S. Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport. Int J Appl Math Theor Phys. 2025;11(2):24-30. doi: 10.11648/j.ijamtp.20251102.11

Copy | Download

@article{10.11648/j.ijamtp.20251102.11,
  author = {Kwang-Ok Ri and Yong-Ho Kim and Chol-U Kim and Jong-Chol Paek and Song-Chol Hong},
  title = {Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport},
  journal = {International Journal of Applied Mathematics and Theoretical Physics},
  volume = {11},
  number = {2},
  pages = {24-30},
  doi = {10.11648/j.ijamtp.20251102.11},
  url = {https://doi.org/10.11648/j.ijamtp.20251102.11},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijamtp.20251102.11},
  abstract = {In this paper, we study the following chemotaxis-Stokes system with active transport  in a bounded domain with positive parameters α, β, χ and λ. Here, c and n denote the density of the nutrient acting as a chemoattractant and the density of the cell, respectively and u denotes the velocity of the fluid. The parameters α, β, χ and λ are positive constants and λ represents the cell growth rate occurred by the nutrient supply. The novelty of this system is that there is not only a chemotaxis term, which reflects the movement of the cells toward nutrient sources, but also an active transport one, which means the nutrient is moving towards the cells. In order to prove the existence of weak solutions to the above problem, we introduce the regularized problem using the the Yosida approximation of B := −∆ + 1 under homogeneous Neumann boundary conditions in L2 (Ω). Based on a priori estimates for the solutions of the regularized problem, it is shown that under no-flux boundary condition and for any suitably regular initial data, an associated initial value problem possesses a global weak solution provided 0 χ < 1.},
 year = {2025}
}

Copy | Download

TY  - JOUR
T1  - Weak Solutions to the Three-Dimensional Chemotaxis-Stokes System with Active Transport
AU  - Kwang-Ok Ri
AU  - Yong-Ho Kim
AU  - Chol-U Kim
AU  - Jong-Chol Paek
AU  - Song-Chol Hong
Y1  - 2025/06/21
PY  - 2025
N1  - https://doi.org/10.11648/j.ijamtp.20251102.11
DO  - 10.11648/j.ijamtp.20251102.11
T2  - International Journal of Applied Mathematics and Theoretical Physics
JF  - International Journal of Applied Mathematics and Theoretical Physics
JO  - International Journal of Applied Mathematics and Theoretical Physics
SP  - 24
EP  - 30
PB  - Science Publishing Group
SN  - 2575-5927
UR  - https://doi.org/10.11648/j.ijamtp.20251102.11
AB  - In this paper, we study the following chemotaxis-Stokes system with active transport  in a bounded domain with positive parameters α, β, χ and λ. Here, c and n denote the density of the nutrient acting as a chemoattractant and the density of the cell, respectively and u denotes the velocity of the fluid. The parameters α, β, χ and λ are positive constants and λ represents the cell growth rate occurred by the nutrient supply. The novelty of this system is that there is not only a chemotaxis term, which reflects the movement of the cells toward nutrient sources, but also an active transport one, which means the nutrient is moving towards the cells. In order to prove the existence of weak solutions to the above problem, we introduce the regularized problem using the the Yosida approximation of B := −∆ + 1 under homogeneous Neumann boundary conditions in L2 (Ω). Based on a priori estimates for the solutions of the regularized problem, it is shown that under no-flux boundary condition and for any suitably regular initial data, an associated initial value problem possesses a global weak solution provided 0 χ < 1.
VL  - 11
IS  - 2
ER  -

Copy | Download