It is well known that every derivation on a von Neumann algebra is inner, which reflects the strong rigidity of these algebras. In contrast, for general C*-algebras there may exist non-inner derivations, indicating a more complicated and diverse algebraic structure. This fundamental difference has stimulated extensive research on derivations on various classes of operator algebras. In recent years, increasing attention has been paid to derivations defined on algebras of unbounded operators, in particular on algebras of measurable, locally measurable, and τ-measurable operators associated with von Neumann algebras. Such algebras arise naturally within the framework of noncommutative integration theory and provide a rich setting for extending classical results from the theory of bounded operators. In particular, a complete description of derivations on these algebras has been established in a number of works when they are associated with type I von Neumann algebras, demonstrating that under appropriate assumptions the derivations possess strong regularity properties and admit explicit representations. The present article is devoted to the development of a real analogue of the results described above. More precisely, derivations on algebras of measurable, locally measurable, and τ-measurable operators associated with real type I von Neumann algebras are investigated. By carefully adapting the methods from the complex case and taking into account the specific algebraic and topological features of real operator algebras, a complete characterization of all derivations on the algebras under consideration is obtained. These results generalize known theorems for complex von Neumann algebras to the real setting and contribute to a deeper understanding of derivations on algebras of unbounded operators associated with real operator algebras.
| Published in | International Journal of Applied Mathematics and Theoretical Physics (Volume 12, Issue 1) |
| DOI | 10.11648/j.ijamtp.20261201.12 |
| Page(s) | 28-33 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2026. Published by Science Publishing Group |
Derivations, Algebra of Measurable Operators, Locally Measurable Operator, -measurable Operator, Von Neumann Algebras
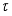 -measurable operators affiliated with von Neumann algebra of type I is given. Papers
-measurable operators affiliated with von Neumann algebra of type I is given. Papers 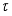 -measurable operators affiliated with real von Neumann algebra of type I are obtained.
-measurable operators affiliated with real von Neumann algebra of type I are obtained. 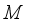 be a *-subalgebra of
be a *-subalgebra of 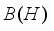 of all bounded linear operators on complex Hilbert space
of all bounded linear operators on complex Hilbert space 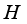 . The set
. The set 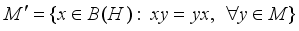 is called the commutant of the *-algebra
is called the commutant of the *-algebra 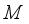 . The set
. The set 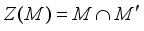 is called the center of the algebra
is called the center of the algebra 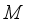 . A *-subalgebra
. A *-subalgebra 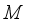 with the property
with the property 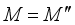 is called W*-algebra, where
is called W*-algebra, where 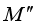 is the double commutant of
is the double commutant of 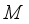 . It is equivalent to that, *-subalgebra
. It is equivalent to that, *-subalgebra 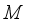 is weakly closed and consists identity (i.e. 1
is weakly closed and consists identity (i.e. 1 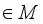 ). W*-algebras are also known as von Neumann Algebras. A W*-algebra
). W*-algebras are also known as von Neumann Algebras. A W*-algebra 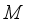 is called a factor if its center is trivial, i.e.
is called a factor if its center is trivial, i.e. 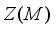 coincides with
coincides with 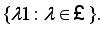
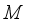 is called discrete, or of type I, if for every nonzero central projection
is called discrete, or of type I, if for every nonzero central projection 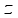 there exists a nonzero abelian projection
there exists a nonzero abelian projection 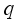 such that
such that 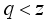 .
. 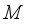 is called of type
is called of type 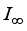 if
if 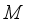 is a nonfinite (infinite) algebra of type I.
is a nonfinite (infinite) algebra of type I. 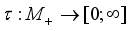 is called a trace on
is called a trace on 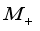 if
if 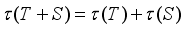 for all
for all 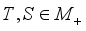 ;
; 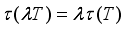 for every
for every 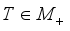 and
and 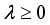 (with the convention
(with the convention 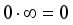 );
); 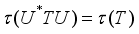 for every
for every 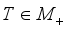 and every unitary operator
and every unitary operator 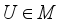 .
. 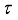 is called finite if
is called finite if 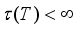 for every
for every 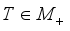 ; semifinite if
; semifinite if 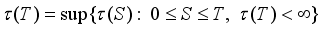 for every
for every 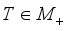 ; faithful if from
; faithful if from 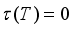 with
with 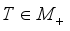 it follows that
it follows that 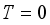 ; normal if from
; normal if from 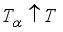 with
with 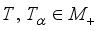 it follows that
it follows that 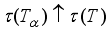 .
. 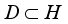 is said to be affiliated with algebra
is said to be affiliated with algebra 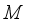 (notation:
(notation: 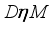 ) if
) if 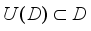 for every unitary operator
for every unitary operator 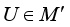 .
. 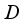 is a closed linear subspace of
is a closed linear subspace of 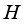 and
and 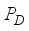 denotes the orthogonal projection onto
denotes the orthogonal projection onto 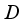 , then
, then 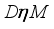 if and only if
if and only if 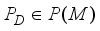 , where
, where 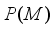 is complete lattice of all projections from
is complete lattice of all projections from 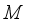 .
. 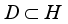 is called strongly dense in
is called strongly dense in 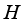 with respect to
with respect to 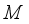 if
if 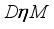 and there exists a sequence of projections
and there exists a sequence of projections 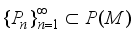
 such that
such that 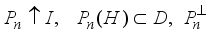 is a finite projection for each
is a finite projection for each 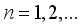 .
. 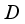 is determined by the sequence of projections
is determined by the sequence of projections 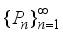 .
. 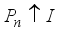 it follows directly that every strongly dense linear subspace is dense in
it follows directly that every strongly dense linear subspace is dense in 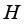 .
. 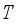 with domain
with domain 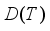 , acting in the Hilbert space
, acting in the Hilbert space 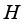 , is called affiliated with
, is called affiliated with 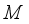 (notation:
(notation: 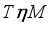 ) if
) if 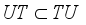 for every unitary
for every unitary 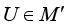 , that is,
, that is, 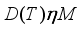 and
and 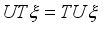 for all
for all 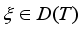 .
. 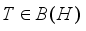 is affiliated with
is affiliated with 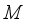 if and only if
if and only if 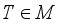 . A closed linear operator
. A closed linear operator 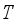 acting in a Hilbert space
acting in a Hilbert space 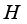 is called measurable with respect to algebra
is called measurable with respect to algebra 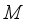 if
if 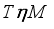 and its domain
and its domain 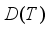 is strongly dense in
is strongly dense in 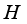 .
. 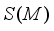 the set of all operators that are measurable with respect to algebra
the set of all operators that are measurable with respect to algebra 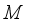 . Clearly,
. Clearly, 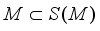 .
. 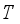 acting in a Hilbert space
acting in a Hilbert space 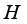 is called locally measurable with respect to algebra
is called locally measurable with respect to algebra 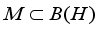 if
if 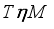 and there exists a sequence of central projections
and there exists a sequence of central projections 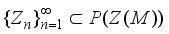 such that
such that 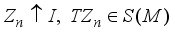 for all
for all 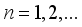 .
. 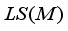 the set of all linear operators that are locally measurable with respect to algebra
the set of all linear operators that are locally measurable with respect to algebra 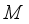 . It is clear that
. It is clear that 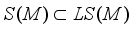 , and
, and 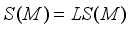 if
if 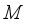 is a factor.
is a factor. 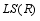 2.2. Derivations on the Algebra
2.2. Derivations on the Algebra 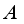 be an algebra over the complex numbers. A linear operator
be an algebra over the complex numbers. A linear operator 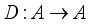 is called a derivation if it satisfies the Leibniz rule
is called a derivation if it satisfies the Leibniz rule 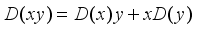 for all
for all 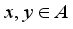 . Every element
. Every element 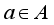 defines a derivation
defines a derivation 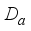 on
on 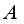 by
by 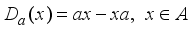 . Such derivations
. Such derivations 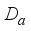 are called inner derivations.
are called inner derivations. 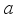 that defines the derivation
that defines the derivation 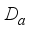 belongs to a larger algebra
belongs to a larger algebra 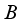 that contains
that contains 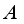 , then
, then 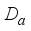 is called a spatial derivation.
is called a spatial derivation. 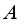 is commutative, all inner derivations are zero, so they are trivial. One of the main problems in the theory of derivations is to determine when derivations are automatically inner or spatial, and whether non-inner derivations exist, especially nontrivial derivations on commutative algebras.
is commutative, all inner derivations are zero, so they are trivial. One of the main problems in the theory of derivations is to determine when derivations are automatically inner or spatial, and whether non-inner derivations exist, especially nontrivial derivations on commutative algebras. 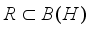 is called real W*-algebra, if it is weakly closed, 1
is called real W*-algebra, if it is weakly closed, 1 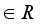 , and
, and 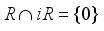 . Real W*-algebras are also known as real von Neumann Algebras. Let
. Real W*-algebras are also known as real von Neumann Algebras. Let 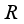 be a real von Neumann algebra and
be a real von Neumann algebra and 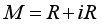 . We consider the algebra
. We consider the algebra 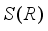 of all measurable operators affiliated with a real von Neumann algebra
of all measurable operators affiliated with a real von Neumann algebra 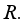 It is proved that (see
It is proved that (see 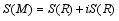 , analogically it is proven that
, analogically it is proven that 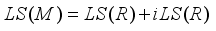 . Below, we give a full description of derivations on the algebra
. Below, we give a full description of derivations on the algebra 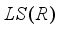 of all locally measurable operators affiliated with a type I real von Neumann algebra
of all locally measurable operators affiliated with a type I real von Neumann algebra  .
. 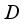 on
on 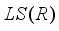 is inner, then it is
is inner, then it is 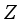 -linear, that is,
-linear, that is, 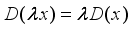 for all
for all 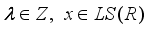 , where
, where 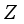 is the center of
is the center of 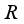 . The following result shows that the opposite statement is also true.
. The following result shows that the opposite statement is also true. 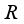 be a type I real von Neumann algebra with the center
be a type I real von Neumann algebra with the center 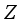 . Then every
. Then every 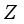 -linear derivation
-linear derivation 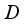 on the algebra
on the algebra 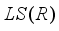 is inner.
is inner. 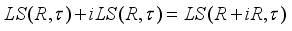 , the derivation
, the derivation 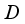 can be extended by
can be extended by 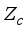 -linearity to derivation
-linearity to derivation 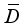 on
on 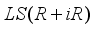 as
as 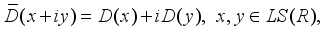
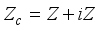 is a center of
is a center of 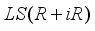 . Since every derivation on
. Since every derivation on 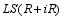 is inner (see
is inner (see 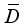 is inner, i.e. there is an element
is inner, i.e. there is an element 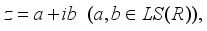 such that
such that 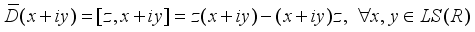 . Then we have
. Then we have 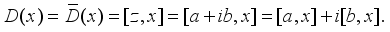
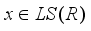 and
and 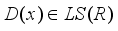 , then
, then 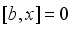 . Hence
. Hence 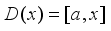 , i.e.
, i.e. 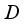 is inner. The theorem is proven.
is inner. The theorem is proven. 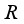 is a type
is a type 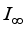 real von Neumann algebra, then any derivation on the algebra
real von Neumann algebra, then any derivation on the algebra 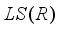 is inner.
is inner. 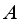 isa commutative algebra and suppose that
isa commutative algebra and suppose that 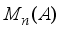 is the algebra of
is the algebra of 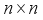 matrices over
matrices over 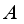 . If
. If 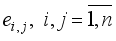 , are the matrix units in
, are the matrix units in 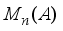 , then every element
, then every element 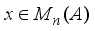 has the form
has the form 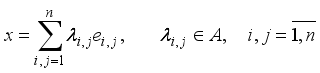 .
. 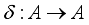 be a derivation. Setting
be a derivation. Setting 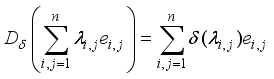 (1)
(1)  on the algebra
on the algebra 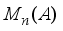 . Moreover
. Moreover 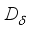 is a derivation on the algebra
is a derivation on the algebra 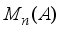 and its restriction onto the center of the algebra
and its restriction onto the center of the algebra 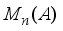 coincides with the given
coincides with the given 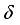 .
. 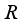 be a homogeneous real von Neumann algebra of type
be a homogeneous real von Neumann algebra of type 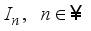 , with the center
, with the center 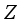 . Since
. Since 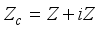 is the center of
is the center of 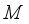 , it follows that
, it follows that 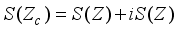 and
and 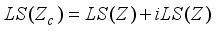 . Let
. Let 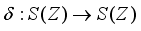 be a derivation and
be a derivation and 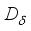 be a derivation on the algebra
be a derivation on the algebra 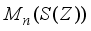 defined by (1). Extend
defined by (1). Extend 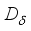 to
to 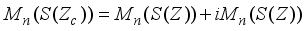 by setting
by setting 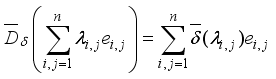 (2)
(2) 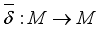 is the extension of
is the extension of 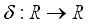 to
to 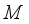 , defined by
, defined by 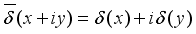 . It is clear that
. It is clear that 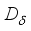 is a derivation on
is a derivation on 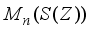 , and
, and 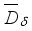 is a derivation on
is a derivation on 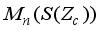 .
. 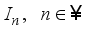 , real von Neumann algebras.
, real von Neumann algebras. 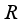 be a homogeneous real von Neumann algebra of type
be a homogeneous real von Neumann algebra of type 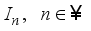 . Each derivation
. Each derivation 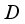 on the algebra
on the algebra 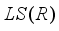 has a unique representation as a sum
has a unique representation as a sum 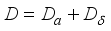
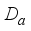 is an inner derivation given by an element
is an inner derivation given by an element 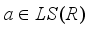 , and
, and 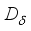 is a derivation of type (1) coming from a derivation
is a derivation of type (1) coming from a derivation 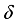 on the center
on the center 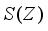 .
. 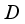 be an arbitrary derivation on the algebra
be an arbitrary derivation on the algebra 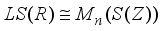 . Now consider the restriction of this derivation
. Now consider the restriction of this derivation 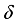 onto the center
onto the center 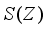 of this algebra, and let
of this algebra, and let 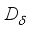 be the derivation on the algebra
be the derivation on the algebra 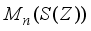 constructed as in (1). Put
constructed as in (1). Put 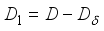 . Then for any
. Then for any 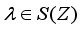 we have
we have 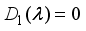 , i.e.
, i.e. 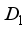 is identically zero on
is identically zero on 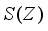 . Therefore
. Therefore 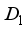 is
is 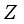 -linear and by Theorem 3.1 we obtain that
-linear and by Theorem 3.1 we obtain that 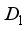 is an inner derivation, and thus
is an inner derivation, and thus 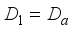 for an appropriate
for an appropriate 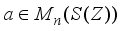 . Therefore
. Therefore 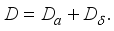 If
If 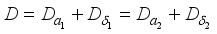 , then
, then 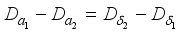 . Since
. Since 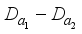 is identically zero on the center of the algebra
is identically zero on the center of the algebra 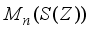 , this implies that
, this implies that 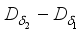 is also identically zero on the center of
is also identically zero on the center of 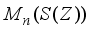 . This means that
. This means that 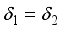 , and therefore
, and therefore 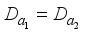 , i.e. the decomposition of
, i.e. the decomposition of 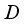 is unique. The proof is complete.
is unique. The proof is complete. 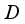 to
to 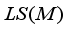 by
by 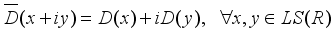 . By Lemma 3.3 (see
. By Lemma 3.3 (see 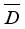 has the form
has the form 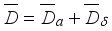 , where
, where 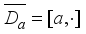 with
with 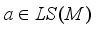 , and
, and 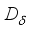 is the derivation defined in (2). From the proof of the Lemma 3.3, it is easy to see that
is the derivation defined in (2). From the proof of the Lemma 3.3, it is easy to see that 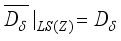 , and for
, and for 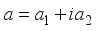 with
with 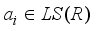 we obtain
we obtain 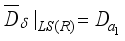 , i.e. we have
, i.e. we have 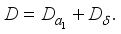
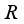 be any finite real von Neumann algebra of type I with the center
be any finite real von Neumann algebra of type I with the center 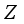 . There exists a family of central projections from
. There exists a family of central projections from 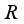 which we denote
which we denote 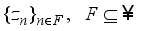 , with
, with 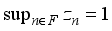 such that the algebra
such that the algebra 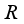 is *-isomorphic to the C*-product of real von Neumann algebras
is *-isomorphic to the C*-product of real von Neumann algebras 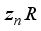 of type
of type 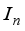 respectively,
respectively, 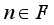 , i.e.
, i.e. 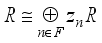 .
. 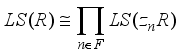 .
. 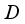 be a derivation on
be a derivation on 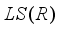 , and
, and 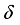 be its restriction onto the center
be its restriction onto the center 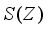 . Since
. Since 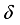 maps each
maps each 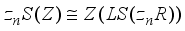 into itself,
into itself, 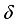 generates a derivation
generates a derivation 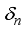 on
on 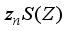 for each
for each 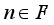 .
. 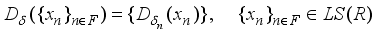 (3)
(3) 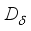 is a derivation on
is a derivation on 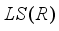 .
. 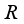 be a finite real von Neumann algebra of type I. Each derivation
be a finite real von Neumann algebra of type I. Each derivation 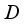 on the algebra
on the algebra 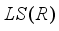 has a unique representation as a sum
has a unique representation as a sum 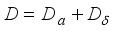
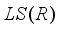 of locally measurable operators with respect to an arbitrary type I real von Neumann algebra
of locally measurable operators with respect to an arbitrary type I real von Neumann algebra 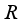 .
. 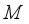 is a type I real von Neumann algebra. There exists a central projection
is a type I real von Neumann algebra. There exists a central projection 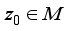 such that
such that 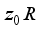 is a finite real von Neumann algebra;
is a finite real von Neumann algebra; 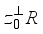 is a real von Neumann algebra of type
is a real von Neumann algebra of type 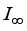 .
. 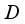 on
on 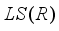 and suppose that
and suppose that 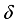 is its restriction onto its center
is its restriction onto its center 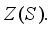 By Theorem 3.2
By Theorem 3.2 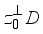 is inner and thus we have
is inner and thus we have 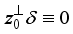 , i.e.
, i.e. 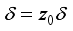 .
. 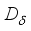 be the derivation on
be the derivation on 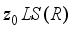 defined as in (3) and consider its extension
defined as in (3) and consider its extension 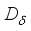 on
on 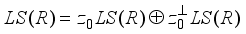
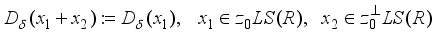 (4)
(4) 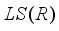 .
. 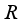 be a type I real von Neumann algebra. Each derivation
be a type I real von Neumann algebra. Each derivation 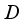 on
on 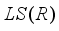 has a unique representation as a sum
has a unique representation as a sum 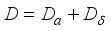
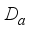 is an inner derivation implemented by an element
is an inner derivation implemented by an element 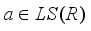 , and
, and 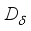 is a derivation of the form (4), generated by a derivation
is a derivation of the form (4), generated by a derivation 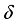 on the center of
on the center of 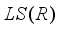 .
. 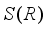 of measurable operators associated with a type I real von Neumann algebra
of measurable operators associated with a type I real von Neumann algebra 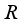 .
. 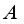 be an arbitrary subalgebra of
be an arbitrary subalgebra of 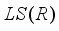 which contains
which contains 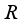 .
. 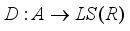 and let us show that
and let us show that 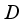 can be extended to a derivation
can be extended to a derivation 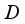 on the whole
on the whole 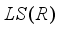 .
. 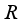 is of type I, for an arbitrary element
is of type I, for an arbitrary element 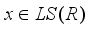 there exists a sequence
there exists a sequence 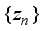 of mutually orthogonal central projections with
of mutually orthogonal central projections with 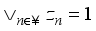 and
and 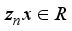 for all
for all 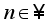 . Set
. Set 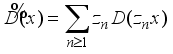 (5)
(5) 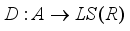 is identically zero on central projections of
is identically zero on central projections of 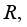 the equality (5) yields a well-defined derivation
the equality (5) yields a well-defined derivation 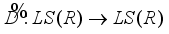 which coincides with
which coincides with 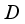 on
on 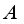 .
. 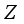 -linearity of
-linearity of 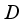 on
on 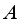 , implies
, implies 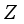 -linearity of
-linearity of 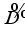 , and by Theorem 3.1 the derivation
, and by Theorem 3.1 the derivation 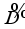 is inner on
is inner on 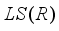 . Therefore
. Therefore 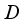 is a spatial derivation on
is a spatial derivation on 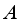 , i.e. there exists an element
, i.e. there exists an element 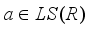 such that
such that 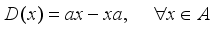 .
. 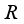 be a type I real von Neumann algebra with the center
be a type I real von Neumann algebra with the center 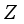 , and let
, and let 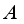 be an arbitrary subalgebra in
be an arbitrary subalgebra in 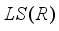 containing
containing 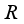 . Then any
. Then any 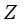 -linear derivation
-linear derivation 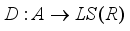 is spatial and implemented by an element of
is spatial and implemented by an element of 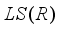 .
. 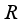 be a type I real von Neumann algebra with the center
be a type I real von Neumann algebra with the center 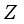 and let
and let 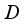 be a
be a 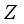 -linear derivation on
-linear derivation on 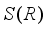 or
or 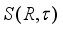 . Then
. Then 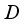 is spatial and implemented by an element of
is spatial and implemented by an element of 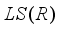 .
. 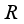 is a type
is a type 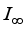 real von Neumann algebra, then every derivation
real von Neumann algebra, then every derivation 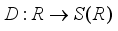 has the form
has the form 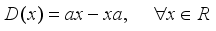 , for an appropriate
, for an appropriate 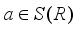 .
. 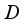 extends to derivation
extends to derivation 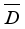 on
on 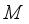 as
as 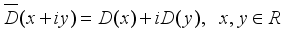 . By Lemma 3.4 (see
. By Lemma 3.4 (see 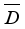 on
on 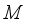 is inner, i.e. there is an element
is inner, i.e. there is an element 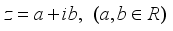 , such that
, such that 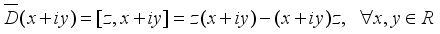 . Then we have
. Then we have 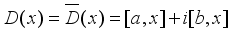 . Since
. Since 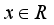 and
and 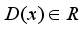 , then
, then 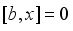 . Hence
. Hence 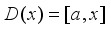 , i.e.
, i.e. 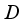 is inner. The Lemma is proven.
is inner. The Lemma is proven. 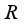 be a type I real von Neumann algebra with the center
be a type I real von Neumann algebra with the center 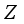 . Then every
. Then every 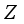 -linear deriva tion
-linear deriva tion 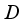 on the algebra
on the algebra 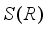 is inner. In particular, if
is inner. In particular, if 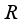 is of type
is of type 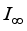 then every derivation on
then every derivation on 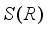 is inner.
is inner. 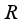 be a type I real von Neumann algebra. Then every derivation
be a type I real von Neumann algebra. Then every derivation 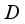 on the algebra
on the algebra 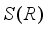 has a unique representation as a sum
has a unique representation as a sum 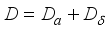
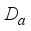 is inner and implemented by an element
is inner and implemented by an element 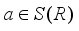 , and
, and 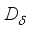 is the derivation of the form (3) generated by a derivation
is the derivation of the form (3) generated by a derivation 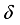 on the center of
on the center of 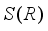 .
. 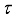 be a faithful normal semifinite trace on a von Neumann algebra
be a faithful normal semifinite trace on a von Neumann algebra 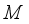 . A linear subspace
. A linear subspace 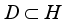 is called
is called 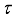 -dense if
-dense if 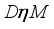 and for every
and for every 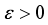 there exists a projection
there exists a projection 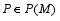 such that
such that 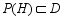 and
and 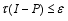 .
. 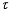 -dense subspace
-dense subspace 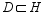 is strongly dense.
is strongly dense. 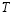 acting in
acting in 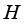 is called
is called 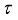 -measurable with respect to algebra
-measurable with respect to algebra 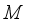 if
if 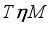 and
and 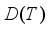 is
is 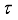 -dense in
-dense in 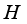 .
. 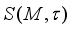 the set of all
the set of all 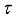 -measurable operators. Clearly,
-measurable operators. Clearly, 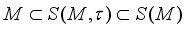 . And
. And 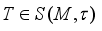 if and only if
if and only if 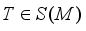 and
and 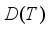 P(T) is
P(T) is 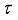 -dense in
-dense in 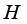 .
. 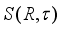 of
of 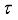 -measurable operators affiliated with a type I real von Neumann algebra
-measurable operators affiliated with a type I real von Neumann algebra 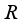 and a faithful normal semifinite trace
and a faithful normal semifinite trace 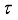 . Similarly to the proof of Theorem 2.1 (see
. Similarly to the proof of Theorem 2.1 (see 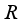 be a type I real von Neumann algebra with the center
be a type I real von Neumann algebra with the center 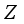 and a faithful normal semi-finite trace. Then every
and a faithful normal semi-finite trace. Then every 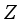 -linear derivation
-linear derivation 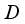 on the algebra
on the algebra 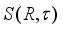 is inner. As a special case, if
is inner. As a special case, if 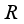 is of type
is of type 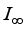 , then every derivation on
, then every derivation on 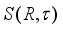 is inner.
is inner. 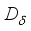 on
on 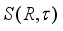 . Now, similarly to Lemma 3.5 one can prove the following.
. Now, similarly to Lemma 3.5 one can prove the following. 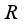 be a finite real von Neumann algebra of type I with a faithful normal semi-finite trace
be a finite real von Neumann algebra of type I with a faithful normal semi-finite trace 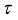 . Each derivation
. Each derivation 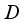 on the algebra
on the algebra 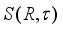 can be uniquely represented in the form
can be uniquely represented in the form 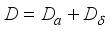 where
where 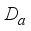 is an inner derivation implemented by an element
is an inner derivation implemented by an element 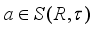 , and
, and 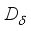 is a derivation given as (5).
is a derivation given as (5). 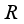 be a type I real von Neumann algebra with a faithful normal semi-finite trace
be a type I real von Neumann algebra with a faithful normal semi-finite trace 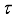 . Then every derivation
. Then every derivation 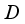 on the algebra
on the algebra 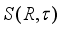 can be uniquely represented in the form
can be uniquely represented in the form 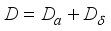 where
where 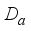 is an inner derivation implemented by an element
is an inner derivation implemented by an element 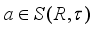 , and
, and 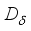 is the derivation from lemma 4.7.
is the derivation from lemma 4.7. 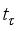 on the algebra
on the algebra 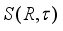 (see Section 1), then it is clear that every non-zero derivation of the form
(see Section 1), then it is clear that every non-zero derivation of the form 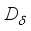 is discontinuous in
is discontinuous in 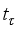 . Therefore, the above Theorem 4.8 implies the following.
. Therefore, the above Theorem 4.8 implies the following. 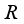 be a type I real von Neumann algebra with a faithful normal semi-finite trace
be a type I real von Neumann algebra with a faithful normal semi-finite trace 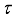 . A derivation
. A derivation 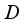 on the algebra
on the algebra 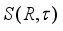 is inner if and only if it is continuous in the measure topology.
is inner if and only if it is continuous in the measure topology. 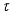 -measurable operators, affiliated with real von Neumann algebra of type I, are obtained.
-measurable operators, affiliated with real von Neumann algebra of type I, are obtained. 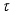 -measurable operators affiliated with von Neumann algebra of type I is obtained. Here, a real analogue of these results is considered. That is, descriptions of derivations on some algebras of measurable, locally measurable, and
-measurable operators affiliated with von Neumann algebra of type I is obtained. Here, a real analogue of these results is considered. That is, descriptions of derivations on some algebras of measurable, locally measurable, and 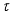 -measurable operators affiliated with real von Neumann algebra of type I are obtained.
-measurable operators affiliated with real von Neumann algebra of type I are obtained. 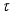 -measurable operators, affiliated with real von Neumann algebra of type I, are obtained.
-measurable operators, affiliated with real von Neumann algebra of type I, are obtained. B(H) | Algebra of all Bounded Linear Operators Acting on a Complex Hilbert Space H |
P(M) | Complete Lattice of all Projections from M |
| [1] | Albeverio S., Ayupov Sh. A., Kudaybergenov K. K., Derivations on the algebra of measurable operators affiliated with a type I von Neumann algebra, Siberian Adv. Math. 2008. No 18. 8694. |
| [2] | Albeverio S., Ayupov Sh. A., Kudaybergenov K. K., Structure of derivations on various algebras of measurable oper?ators, J. Funct. Anal. 2009, 252. 2917-2943. |
| [3] | S. Albeverio, Sh. A. Ayupov, K. K. Kudaybergenov. Local Derivations on Algebras of Measurable Operators. Comm. Contemp. Math., 2011. Vol. 13, No. 4 (2011) 1-15. |
| [4] | Ayupov Sh. A., Kudaybergenov K. K., Innerness of continuous derivations on algebras of measurable operators affili?ated with finite von Neumann algebras. Journal of Mathematical Analysis and Applications. 408/1, (2013), 256-267. |
| [5] | Ayupov Sh. A, Rakhimov A.A, Usmanov Sh. M. Jordan, Real and Lie Structures in Operator Algebras, Kluw.Acad.Pub., MAIA, 1997, 418, 235p. |
| [6] | A. F. Ber, V. I. Chilin, F. A. Sukochev. Continuity of derivations in algebras of locally measurable operators. Integr. Equ. Oper. Theory / Proc. Lond. Math. Soc. 2013. |
| [7] | A. F. Ber, V. I. Chilin, F. A. Sukochev. Innerness of continuous derivations on algebras of locally measurable operators. Proc. London Math. Soc., 2014. |
| [8] | A. F. Ber, B. de Pagter, F. A. Sukochev. Some remarks on derivations in algebras of measurable operators. Math. Notes, 2010. |
| [9] | Muratov M. A., Chilin V. I., Topological algebras of measurable and locally measurable operators, CMFD, 2016, 61. 115-163. |
| [10] | Karimov U.Sh., Algebra of measurable operators affiliated with finite real W*-algebras and its derivations. Bull.Math.Inst. 2025. Vol 8. Issue 6. 161-165. |
APA Style
Rakhimov, A., Karimov, U. (2026). Derivations on Some Algebras of Measurable Operators Affiliated with Real W*-algebras of Type I. International Journal of Applied Mathematics and Theoretical Physics, 12(1), 28-33. https://doi.org/10.11648/j.ijamtp.20261201.12
ACS Style
Rakhimov, A.; Karimov, U. Derivations on Some Algebras of Measurable Operators Affiliated with Real W*-algebras of Type I. Int. J. Appl. Math. Theor. Phys. 2026, 12(1), 28-33. doi: 10.11648/j.ijamtp.20261201.12
@article{10.11648/j.ijamtp.20261201.12,
author = {Abdugafur Rakhimov and Ulugbek Karimov},
title = {Derivations on Some Algebras of Measurable Operators Affiliated with Real W*-algebras of Type I},
journal = {International Journal of Applied Mathematics and Theoretical Physics},
volume = {12},
number = {1},
pages = {28-33},
doi = {10.11648/j.ijamtp.20261201.12},
url = {https://doi.org/10.11648/j.ijamtp.20261201.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijamtp.20261201.12},
abstract = {It is well known that every derivation on a von Neumann algebra is inner, which reflects the strong rigidity of these algebras. In contrast, for general C*-algebras there may exist non-inner derivations, indicating a more complicated and diverse algebraic structure. This fundamental difference has stimulated extensive research on derivations on various classes of operator algebras. In recent years, increasing attention has been paid to derivations defined on algebras of unbounded operators, in particular on algebras of measurable, locally measurable, and τ-measurable operators associated with von Neumann algebras. Such algebras arise naturally within the framework of noncommutative integration theory and provide a rich setting for extending classical results from the theory of bounded operators. In particular, a complete description of derivations on these algebras has been established in a number of works when they are associated with type I von Neumann algebras, demonstrating that under appropriate assumptions the derivations possess strong regularity properties and admit explicit representations. The present article is devoted to the development of a real analogue of the results described above. More precisely, derivations on algebras of measurable, locally measurable, and τ-measurable operators associated with real type I von Neumann algebras are investigated. By carefully adapting the methods from the complex case and taking into account the specific algebraic and topological features of real operator algebras, a complete characterization of all derivations on the algebras under consideration is obtained. These results generalize known theorems for complex von Neumann algebras to the real setting and contribute to a deeper understanding of derivations on algebras of unbounded operators associated with real operator algebras.},
year = {2026}
}
TY - JOUR T1 - Derivations on Some Algebras of Measurable Operators Affiliated with Real W*-algebras of Type I AU - Abdugafur Rakhimov AU - Ulugbek Karimov Y1 - 2026/01/27 PY - 2026 N1 - https://doi.org/10.11648/j.ijamtp.20261201.12 DO - 10.11648/j.ijamtp.20261201.12 T2 - International Journal of Applied Mathematics and Theoretical Physics JF - International Journal of Applied Mathematics and Theoretical Physics JO - International Journal of Applied Mathematics and Theoretical Physics SP - 28 EP - 33 PB - Science Publishing Group SN - 2575-5927 UR - https://doi.org/10.11648/j.ijamtp.20261201.12 AB - It is well known that every derivation on a von Neumann algebra is inner, which reflects the strong rigidity of these algebras. In contrast, for general C*-algebras there may exist non-inner derivations, indicating a more complicated and diverse algebraic structure. This fundamental difference has stimulated extensive research on derivations on various classes of operator algebras. In recent years, increasing attention has been paid to derivations defined on algebras of unbounded operators, in particular on algebras of measurable, locally measurable, and τ-measurable operators associated with von Neumann algebras. Such algebras arise naturally within the framework of noncommutative integration theory and provide a rich setting for extending classical results from the theory of bounded operators. In particular, a complete description of derivations on these algebras has been established in a number of works when they are associated with type I von Neumann algebras, demonstrating that under appropriate assumptions the derivations possess strong regularity properties and admit explicit representations. The present article is devoted to the development of a real analogue of the results described above. More precisely, derivations on algebras of measurable, locally measurable, and τ-measurable operators associated with real type I von Neumann algebras are investigated. By carefully adapting the methods from the complex case and taking into account the specific algebraic and topological features of real operator algebras, a complete characterization of all derivations on the algebras under consideration is obtained. These results generalize known theorems for complex von Neumann algebras to the real setting and contribute to a deeper understanding of derivations on algebras of unbounded operators associated with real operator algebras. VL - 12 IS - 1 ER -