Channel estimation for millimeter wave (mmWave) hybrid MIMO communications, is challenging because of the complexities associated with the large antenna arrays at the transceivers and with the higher propagation lossess of the mmWaves. However, with open-loop training and exploiting the inherent sparse nature of the mmWave channel, it becomes easier by formulating the channel estimation problem in compressive sensing (CS) theory, and solving the problem using orthogonal matching pursuit (OMP) algorithm. In the CS theory, coherence and restricted isometry property (RIP) of sensing matrices, and restricted isometry constant (RIC) based k-sparse signal recovery exactly in k iterations, are significant conditions for guaranteed recoverability. Most of the earlier works are focused on coherence only, because of the impracticality of computation of RICs for the larger dimensional mmWave channel. In this paper, a novel technique, for the first time different from the earlier works, is devised to achieve guaranteed open-loop training based channel estimation. As there is hurdle for computation of RIC for the channel, smaller dimensional sensing (DFT) matrices are synthesized and are subjected for guaranteed recoverability conditions. From the simulation results of recoverability with synthesized and channel matrices, guarantee of the mmWave channel estimation is achieved.
| Published in | International Journal of Wireless Communications and Mobile Computing (Volume 12, Issue 1) |
| DOI | 10.11648/j.wcmc.20251201.15 |
| Page(s) | 46-54 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
mmWaves, Channel Estimation, Hybrid MIMO Communications, Open-loop Methods, Compressive Sensing, OMP, Coherence and RIP, Sparse Signal Recovery in K-iterations
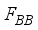 ) and an analog RF precoder(denoted by
) and an analog RF precoder(denoted by 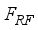 ) with
) with 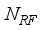 chains, connected to
chains, connected to 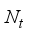 transmitting antennas, and the receiver is equipped with
transmitting antennas, and the receiver is equipped with 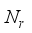 receiving antennas connected to an analog RF combiner (denoted by
receiving antennas connected to an analog RF combiner (denoted by 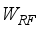 ) with
) with 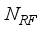 chains and a digital baseband processor (denoted by
chains and a digital baseband processor (denoted by 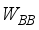 ), for communication of
), for communication of 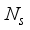 data streams, such that
data streams, such that 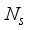 ≤
≤ 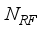 ≤
≤ 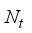 at the transmitter and
at the transmitter and 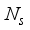 ≤
≤ 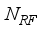 ≤
≤ 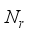 at the receiver respectively.
at the receiver respectively. 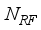 chains are capable of generating
chains are capable of generating 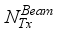 (
( 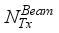 ≤
≤ 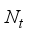 ), denoted by
), denoted by 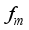
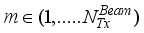 , and at the receiver, the
, and at the receiver, the 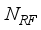 chains are capable of receiving
chains are capable of receiving 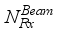 , denoted by
, denoted by 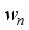
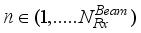 . During the training period,
. During the training period, 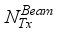 are sent successively, one after the other, and in the receiver each transmitted beam is received as
are sent successively, one after the other, and in the receiver each transmitted beam is received as 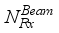 simultaneously through Nr antennas.
simultaneously through Nr antennas. 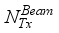 and
and 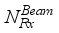 are chosen as multiples of
are chosen as multiples of 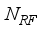 chains and hence rf chains generate transmitter blocks as
chains and hence rf chains generate transmitter blocks as 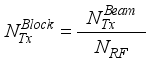 and receiver blocks as,
and receiver blocks as, 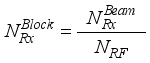 .
. 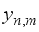 .Collecting all
.Collecting all 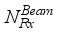 the received vector for a single (mth) transmitted beam is denoted as
the received vector for a single (mth) transmitted beam is denoted as 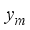 . With the training pilot symbols, X, representing the received signal vector in matrix form for all the transmitted beams,
. With the training pilot symbols, X, representing the received signal vector in matrix form for all the transmitted beams, 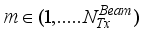 , it is given as
, it is given as 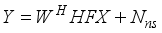 (1)
(1) 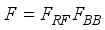 ), combining matrices (
), combining matrices ( 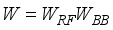 ), channel, (H), and noise (
), channel, (H), and noise ( 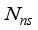 ) are parameters of Y, in (1). When, X is assumed as
) are parameters of Y, in (1). When, X is assumed as 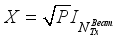 , where P is the pilot power, the received signal vector is represented as
, where P is the pilot power, the received signal vector is represented as 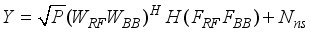 (2)
(2) 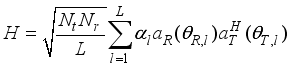 (3)
(3)  are complex gains and L are propagation paths.And assuming uniform linear array (ULA) at both the transmitter and receiver, the antenna steering vectors,
are complex gains and L are propagation paths.And assuming uniform linear array (ULA) at both the transmitter and receiver, the antenna steering vectors, 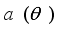 are represented as
are represented as 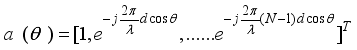 (4)
(4) 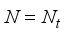 and
and 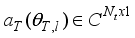 is the steering vector, at the transmitter and,
is the steering vector, at the transmitter and, 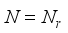 , and
, and 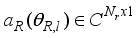 is the steering vector at the receiving antenna.
is the steering vector at the receiving antenna. 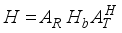 (5)
(5) 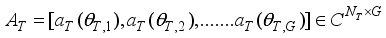 (6)
(6) 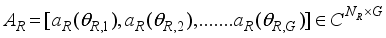 (7)
(7) 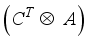 .vec(B),(8)
.vec(B),(8) 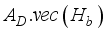 =
= 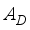 .
. 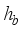 , (9)
, (9) 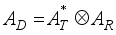 and
and 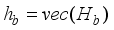 .
. 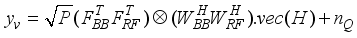
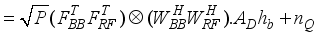
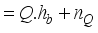 (10)
(10) 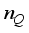 is resultant noise term after vectorization, and
is resultant noise term after vectorization, and 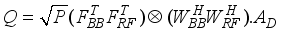 (11)
(11) 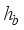 ), is the sparse signal (channel) to be recovered.
), is the sparse signal (channel) to be recovered. 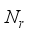 and ad nearlyequal to
and ad nearlyequal to 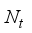 to reduce the redundant dictionaries (
to reduce the redundant dictionaries ( 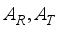 ) to approximately orthogonal dictionaries, as shown by
) to approximately orthogonal dictionaries, as shown by 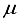 ) and restricted isometry property (RIP) of any sensing matrix, are significant parameters for sparse signal recovery. Lower coherence, and fulfilling RIP are wellness conditions of matrices, for guaranteed recoverability.
) and restricted isometry property (RIP) of any sensing matrix, are significant parameters for sparse signal recovery. Lower coherence, and fulfilling RIP are wellness conditions of matrices, for guaranteed recoverability. 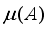 )
) 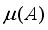 , of matrixA, is defined as the largest absolute inner product between any two columns,
, of matrixA, is defined as the largest absolute inner product between any two columns, 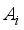 ,
, 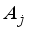 , and is given as
, and is given as 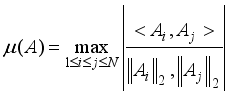 (12)
(12) 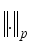 , is
, is 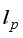 -norm for respective p (p=0,1,2,
-norm for respective p (p=0,1,2, 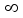 ). Let a matrix, A, of size MxN, and M<N, (N>2), whose columns are normalized, i.e.
). Let a matrix, A, of size MxN, and M<N, (N>2), whose columns are normalized, i.e. 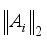 =1,
=1, 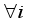 , then the bounds of the coherence index of A, satisfies,
, then the bounds of the coherence index of A, satisfies, 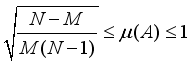 (13)
(13) 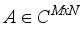 , is said to satisfy the RIP of order k with a constant
, is said to satisfy the RIP of order k with a constant 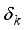
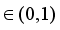 if the following holds:
if the following holds: 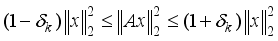 (14)
(14) 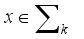 , where
, where 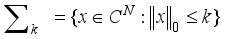 is the set of all k-sparse vectors in
is the set of all k-sparse vectors in 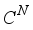 . Constants
. Constants 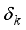
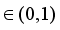 satisfying the above equation for sparsity levels k are called as restricted isometry constants (RICs).In particular, the minimum of all constants δ satisfying the above equation is called the s‐order Restricted Isometry Constant (RIC) and denoted by δs.
satisfying the above equation for sparsity levels k are called as restricted isometry constants (RICs).In particular, the minimum of all constants δ satisfying the above equation is called the s‐order Restricted Isometry Constant (RIC) and denoted by δs. 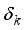 ) satisfy
) satisfy 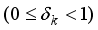 and for sparsity levels, k=1,2,3……. it satisfy
and for sparsity levels, k=1,2,3……. it satisfy 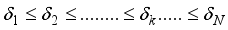 .
. 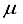 ), and restricted isometry constants (RICs), are computed. From the RICs,
), and restricted isometry constants (RICs), are computed. From the RICs, 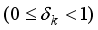 , sparsity level, k is obtained.
, sparsity level, k is obtained. 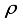 ) for a matrix, A of size, (MxN) is taken as ratio of M to N, i.e. (
) for a matrix, A of size, (MxN) is taken as ratio of M to N, i.e. ( 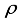 =M/N), for representation of specific properties of sensing matrices.
=M/N), for representation of specific properties of sensing matrices. 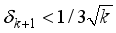 (15)
(15) 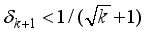 (16)
(16) 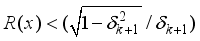 , where
, where 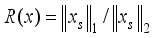 ), on the signal, x, OMP can also exactly recover the signal if RIC, satisfies
), on the signal, x, OMP can also exactly recover the signal if RIC, satisfies 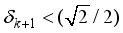 = 0.707(17)
= 0.707(17) 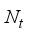 =28, and
=28, and 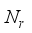 =36 respectively, for a single uplink mmwave hybrid MIMO communication. For input,
=36 respectively, for a single uplink mmwave hybrid MIMO communication. For input, 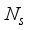 =4, data streams, Rf chains at the transmitter and receiver are as:
=4, data streams, Rf chains at the transmitter and receiver are as: 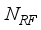 =4.As described in section-II, for each transmitted beam, the number of receive beams and the blocks developed by the rf chains, are with the selection of
=4.As described in section-II, for each transmitted beam, the number of receive beams and the blocks developed by the rf chains, are with the selection of 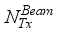 =
= 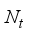 ,
, 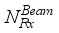 =
= 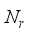 . The number of propagation paths, L= 11, (sufficiently more than the experimentally observed sparsity, (3 to 5), of the mmWave channel) and the angular space grid resolution, G, is taken as 36. With these parameters, as described in section-II, precoder, and combiner matrices are designed in DFT matrices and by formulating the channel estimation problem in CS theory, the resulted sensing matrix, Q, (eq.9) of dimension (1008x1296), is obtained. As described at the end of Section-II, channel is estimated for sparsity level, k=11, using OMP algorithm and the estimation ofdominant paths of the mmWave channel, is shown in Figure 2.
. The number of propagation paths, L= 11, (sufficiently more than the experimentally observed sparsity, (3 to 5), of the mmWave channel) and the angular space grid resolution, G, is taken as 36. With these parameters, as described in section-II, precoder, and combiner matrices are designed in DFT matrices and by formulating the channel estimation problem in CS theory, the resulted sensing matrix, Q, (eq.9) of dimension (1008x1296), is obtained. As described at the end of Section-II, channel is estimated for sparsity level, k=11, using OMP algorithm and the estimation ofdominant paths of the mmWave channel, is shown in Figure 2. 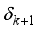 ) should be less than
) should be less than 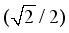 , i.e 0.707. In our analysis, for a matrix, A1, of size, (14x18), having a sparsity, k=11, rho=0.7777, and RIC value obtained is 0.387. It satisfies the limit given by
, i.e 0.707. In our analysis, for a matrix, A1, of size, (14x18), having a sparsity, k=11, rho=0.7777, and RIC value obtained is 0.387. It satisfies the limit given by 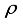 =0.75, satisfying conditions for recovery in k-iterations and success rate of more than 98%.
=0.75, satisfying conditions for recovery in k-iterations and success rate of more than 98%. 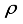 =0.75, success rate and guaranteed recovery in k-iterations.
=0.75, success rate and guaranteed recovery in k-iterations. 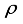 =-.7777, recovery success rate and sparse recovery in k-iterations, the specified guaranteed conditions, are applicable for both A1 and Q in this set. Thus from Figure 3, and Figure 4, guarantee of the mmWave channel is achieved.
=-.7777, recovery success rate and sparse recovery in k-iterations, the specified guaranteed conditions, are applicable for both A1 and Q in this set. Thus from Figure 3, and Figure 4, guarantee of the mmWave channel is achieved. MIMO | Multiple Input and Multiple Output |
DFT | Discrete Fourier Transform |
| [1] | Z. Pi and F. Khan, “An introduction to millimeter-wave mobile broadband systems,” IEEE Commun. Mag., vol. 49, no.6, pp. 101–107, 2011. |
| [2] | T. S. Rappaport, S. Sun, R. Mayzus, H. Zhao, Y. Azar, K. Wang, G. Wong, J. Schulz, M. Samimi, and F. Gutierrez,“ Millimeter wave mobile communications for 5G cellular: It will work!”, IEEE Access, vol. 1, pp. 335–349, 2013. |
| [3] | Rappaport, T. S., Xing, Y., Maccartney, G., et al., “Overview of millimeter wave communications for fifth-generation (5G) wireless networks - With a focus on propagation models”, IEEE Transactions on Antennas and Propagation, vol. 65, no. 12, p. 6213–6230, 2017. |
| [4] | Zhenyu Xiao et.al., “ Channel Estimation and Hybrid Precoding for Millimeter-Wave MIMO Systems: A Low-Complexity Overall Solution”, |
| [5] | Roh, W., Seol, J., Park, J., Lee, B., Lee, J., & Kim, Y. et al., “Millimeter-wave beamforming as an enabling technology for 5G cellular communications: theoretical feasibility and prototype results”, IEEE Communications [Magazine, 52(2), 106-113, 2014. |
| [6] | Swindlehurst, A., Ayanoglu, E., Heydari, P., & Capolino, F., “Millimeter-wave massive MIMO: the next wireless revolution?”, IEEE Communications Magazine, 52(9), 56-62, 2014. |
| [7] | R. W. Heath, N. González-Prelcic, S. Rangan, W. Roh, and A. M. Sayeed, “An overview of signal processing techniques for millimeter wave MIMOsystems,” IEEE J. Sel. Topics Signal Process, vol. 10, no. 3, pp. 436–453, 2016. |
| [8] | J. Zhang, A.Wiesel, and M. Haardt, “Low rank approximation based hybrid precoding schemes for multi-carrier single-user massive MIMO systems,” in Proc. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP)”, pp. 3281–3285, 2016. |
| [9] | J. Zhang, I. Podkurkov, M. Haardt, and A. Nadeev, “Channel estimation and training design for hybrid analog-digital multicarrier single-user massive MIMO systems,” in Proc. 20th International ITG Workshop on Smart Antennas (WSA), pp. 1–8, 2016. |
| [10] | R. Mendez-Rial, N. González-Prelcic, A. Alkhateeb, and R.W.Heath, “Hybrid MIMO architectures for millimeter wave communications: Phase shifters or switches?,” IEEE Access, vol. 4, pp. 247–267, 2016. |
| [11] | K. Ardah, G. Fodor, Y. C. B. Silva, W. Cruz, and F. R. Cavalcanti, “A unifying design of hybrid beamforming architectures employing phase-shifters or switches,” IEEE Trans. Veh. Technol., pp. 1–1, 2018. |
| [12] | O. El Ayach, R. W. Heath, Jr., S. Abu-Surra, S. Rajagopal, and Z. Pi, “Low complexity precoding for large millimeter wave MIMO systems,” in Proc. IEEE Int. Conf. Commun., pp., 2012. |
| [13] | Khaled Ardahz, Bruno Sokalz, André L. F. de Almeiday, and Martin Haardtz, “Compressedsensing based channel estimation and open-loop training design for hybrid analog -digital massive MIMO systems”, 2020. |
| [14] | IEEE P802.11.ad, Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications - Amendment 3: Enhancements for Very High Throughput in the 60GHz band, Jan. 2013. |
| [15] | IEEE 802 Part 15.3: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for High Rate Wireless Personal Area Networks (WPANs) - Amendment 2: Millimeter-wave based Alternative Physical Layer Extension, Oct. 2009. |
| [16] | J. Lee, G. Gil, and Y. H. Lee, “Channel estimation via orthogonal matching pursuit for hybrid MIMO systems in millimeter wave communications,” IEEE Trans. Commun., vol. 64, no. 6, pp.2370–2386, 2016. |
| [17] | L. Wei, R.Q. Hu, Y. Qian, G. Wu, Key elements to enable millimeter wave communications for 5G wireless systems, IEEE Wirel. Commun. 21 (6) (2014) 136–143. |
| [18] | A. Alkhateeb, O. ElAyach, G. Leus, and R.W. Heath, “Channel estimation and hybrid precoding for millimeter wave cellular systems,” IEEE J. Sel. Topics Signal Process., vol. 8, no. 5, pp. 831–846, 2014. |
| [19] | Z. Gao, L. Dai, D. Mi, Z. Wang, M.A. Imran, M.Z. Shakir, MmWave massive MIMO based wireless backhaul for 5G ultra-dense network, IEEE Wirel. Commun. 22(5) (2015) 13–21. |
| [20] | S. Han, I. Chih-Lin, Z. Xu, C. Rowell, Large-scale antenna systems with hybrid precoding analog and digital beamforming for millimter wave 5G, IEEE Commun. Mag. 53(1) (2015) 186–194. |
| [21] | T. Rappaport, F. Gutierrez, E. Ben-Dor, J. Murdock, Y. Qiao, and J. Tamir, “Broadband millimeter-wave propagation measurements and models using adaptive-beam antennas for outdoor urban cellular communications,”IEEE Transactions on Antennas and Propagation, vol. 61, no. 4, pp. 1850–1859, 2013. |
| [22] | A. Sayeed and V. Raghavan, “Maximizing MIMO capacity in sparse multipath with reconfigurable antenna arrays,” IEEE Journal of Selected Topics in Signal Processing, vol. 1, no. 1, pp. 156–166, 2007. |
| [23] | T. Rappaport, Y. Qiao, J. Tamir, J. Murdock, and E. Ben-Dor, “Cellular broadband millimeter wave propagation and angle of arrival for adaptive beam steering systems,” in Radio and Wireless Symposium (RWS), Santa Clara, CA, January 2012, pp. 151–154. |
| [24] | H. Zhang, S. Venkateswaran, and U. Madhow, “Channel modeling and MIMO capacity for outdoor millimeter wave links,” in Proc. of Wireless Communications and Networking Conference (WCNC), Sydney, NSW, April 2010, pp. 1–6. |
| [25] | Ma, X., Yang, F., Liu, S., et al., “ Design and optimization on training sequence for mmwave communications: A new approach for sparse channel estimation in massive MIMO”, IEEE Journal on Selected Areas in Communications, vol. 35, no. 7, p. 1486–1497, 2017. |
| [26] | Faisal AKRAM, et al., “Coherence Optimized Channel Estimation for Mm-Wave Massive MIMO”, RadioEngineering, VOL. 29, NO. 4, December, 2020. |
| [27] | S. Foucart and H. Rauhut, “A Mathematical Introduction to Compressive Sensing”, Birkhäuser, 2013. |
| [28] | E. Cand`es and T. Tao, “Decoding by linear programming,” IEEE Trans.Inf. Theory, vol. 51, no. 12, pp. 4203–4215, Dec. 2005. |
| [29] | E. Cand`es and T. Tao, “Near-optimal signal recovery from random projections: universal encoding strategies?,” IEEE Trans. Inf. Theory, vol. 52, no. 12, pp. 5406–5425, 2006. |
| [30] | M. Rudelson and R. Vershynin, “Sparse reconstruction by convex relaxation: Fourier and gaussian measurements,” in 40th Annual Conference on Information Sciences and Systems, 2006, pp. 207–212. |
| [31] | M.F. Duarte and Y.C. Eldar, “Structured compressed sensing: From theory to applications,” IEEE Trans. Signal Process., vol. 59, no. 9, pp. 4053 –4085, Sept. 2011. |
| [32] | J. A. Tropp and A. C. Gilbert, “Signal recovery from random measurements via orthogonal matching pursuit,” IEEE Trans. Inf. Theory, vol.53, no. 12, pp. 4655–4666, 2007. |
| [33] | J. A. Tropp, “Greed is good: Algorithmic results for sparse approximation,” IEEE Trans. Inf. Theory, vol. 50, no. 10, pp. 22312242, Oct.2004. |
| [34] | A. Fletcher and S. Rangan, “Orthogonal matching pursuit from noisy random measurements: A new analysis,” in Advances in Neural Information Processing Systems 23, Vancouver, 2009. |
| [35] | M.A. Davenport and M.B. Wakin, “Analysis of orthogonal matching pursuit using the restricted isometry property,” IEEE Trans. Inf. Theory, vol. 56, no. 9, pp. 4395 –4401, sept. 2010. |
| [36] | J. Wang and B. Shim, “On the recovery limit of sparse signals using orthogonal matching pursuit,” IEEE Trans. Signal Process., vol. 60, no.9, pp. 4973–4976, Sept. 2012. |
| [37] | L.-H. Chang and J.-Y. Wu, “An improved RIP-based performance guar-antee for sparse signal recovery via orthogonal matching pursuit,” IEEE Trans. Inf. Theory, vol. 60, no. 9, pp. 707–710, 2014. |
| [38] | J. Wen, Z. Zhou, Z. Liu, et al. “Sharp Sufficient Conditions for Stable Recovery of Block Sparse Signals by Block Orthogonal Matching Pur-suit,” 2016, |
| [39] | Xueping Chen et.al., “A note on orthogonal matching pursuit under restricted isometry property”, IET Signal Processing, |
| [40] | Chang Liu et.al., “Some New Results about Sufficient Conditions for Exact Support Recovery of Sparse Signals via Orthogonal Matching Pursuit”, |
APA Style
Pattem, A. (2025). Guaranteed Open-loop Channel Estimation for mmWave Hybrid MIMO Communications, Using Orthogonal Matching Pursuit (OMP) Algorithm. International Journal of Wireless Communications and Mobile Computing, 12(1), 46-54. https://doi.org/10.11648/j.wcmc.20251201.15
ACS Style
Pattem, A. Guaranteed Open-loop Channel Estimation for mmWave Hybrid MIMO Communications, Using Orthogonal Matching Pursuit (OMP) Algorithm. Int. J. Wirel. Commun. Mobile Comput. 2025, 12(1), 46-54. doi: 10.11648/j.wcmc.20251201.15
@article{10.11648/j.wcmc.20251201.15,
author = {Anjaneyulu Pattem},
title = {Guaranteed Open-loop Channel Estimation for mmWave Hybrid MIMO Communications, Using Orthogonal Matching Pursuit (OMP) Algorithm
},
journal = {International Journal of Wireless Communications and Mobile Computing},
volume = {12},
number = {1},
pages = {46-54},
doi = {10.11648/j.wcmc.20251201.15},
url = {https://doi.org/10.11648/j.wcmc.20251201.15},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.wcmc.20251201.15},
abstract = {Channel estimation for millimeter wave (mmWave) hybrid MIMO communications, is challenging because of the complexities associated with the large antenna arrays at the transceivers and with the higher propagation lossess of the mmWaves. However, with open-loop training and exploiting the inherent sparse nature of the mmWave channel, it becomes easier by formulating the channel estimation problem in compressive sensing (CS) theory, and solving the problem using orthogonal matching pursuit (OMP) algorithm. In the CS theory, coherence and restricted isometry property (RIP) of sensing matrices, and restricted isometry constant (RIC) based k-sparse signal recovery exactly in k iterations, are significant conditions for guaranteed recoverability. Most of the earlier works are focused on coherence only, because of the impracticality of computation of RICs for the larger dimensional mmWave channel. In this paper, a novel technique, for the first time different from the earlier works, is devised to achieve guaranteed open-loop training based channel estimation. As there is hurdle for computation of RIC for the channel, smaller dimensional sensing (DFT) matrices are synthesized and are subjected for guaranteed recoverability conditions. From the simulation results of recoverability with synthesized and channel matrices, guarantee of the mmWave channel estimation is achieved.
},
year = {2025}
}
TY - JOUR T1 - Guaranteed Open-loop Channel Estimation for mmWave Hybrid MIMO Communications, Using Orthogonal Matching Pursuit (OMP) Algorithm AU - Anjaneyulu Pattem Y1 - 2025/06/23 PY - 2025 N1 - https://doi.org/10.11648/j.wcmc.20251201.15 DO - 10.11648/j.wcmc.20251201.15 T2 - International Journal of Wireless Communications and Mobile Computing JF - International Journal of Wireless Communications and Mobile Computing JO - International Journal of Wireless Communications and Mobile Computing SP - 46 EP - 54 PB - Science Publishing Group SN - 2330-1015 UR - https://doi.org/10.11648/j.wcmc.20251201.15 AB - Channel estimation for millimeter wave (mmWave) hybrid MIMO communications, is challenging because of the complexities associated with the large antenna arrays at the transceivers and with the higher propagation lossess of the mmWaves. However, with open-loop training and exploiting the inherent sparse nature of the mmWave channel, it becomes easier by formulating the channel estimation problem in compressive sensing (CS) theory, and solving the problem using orthogonal matching pursuit (OMP) algorithm. In the CS theory, coherence and restricted isometry property (RIP) of sensing matrices, and restricted isometry constant (RIC) based k-sparse signal recovery exactly in k iterations, are significant conditions for guaranteed recoverability. Most of the earlier works are focused on coherence only, because of the impracticality of computation of RICs for the larger dimensional mmWave channel. In this paper, a novel technique, for the first time different from the earlier works, is devised to achieve guaranteed open-loop training based channel estimation. As there is hurdle for computation of RIC for the channel, smaller dimensional sensing (DFT) matrices are synthesized and are subjected for guaranteed recoverability conditions. From the simulation results of recoverability with synthesized and channel matrices, guarantee of the mmWave channel estimation is achieved. VL - 12 IS - 1 ER -